Результаты численного анализа

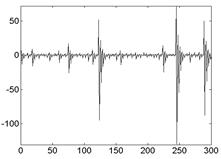
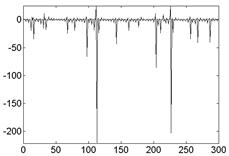
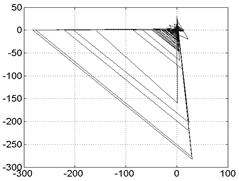
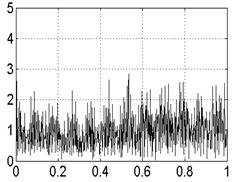
4.1. Реализации отображения перемежаемости (формулы (1.13), (1.14)) представляют собой сигналы типа “накопление- выброс” (рис. 1.). Соответствующие фазовый портрет и спектр мощности представлены на рис. 2.

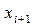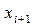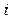
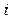
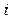а) б)

Рис.1. Реализации отображения перемежаемости. а) 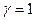, , 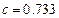б) , .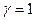

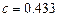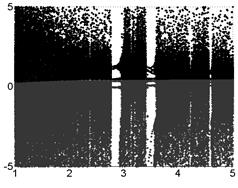
Полученное нами отображение реализует особый тип перемежаемости – хаотические выбросы большой амплитуды на фоне мелкомасштабных осцилляций. Поэтому на рис. 3. показан только фрагмент бифуркационной диаграммы для -5<x<5. По принятому условию возможности автоколебательности процесса (цикл 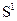) 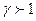. Сразу начиная с 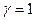имеет место хаотический режим. В интервале 2< 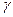<3 наблюдаются первые окна периодичности в хаосе.

Видны типичные картины удвоения периода по Фейгенбауму (цикл 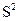). Некоторые ветви наклонных линий бифуркации удвоения не реализованы, процесс имеет асимметрию.

Почти горизонтальные линии соответствуют самой сложной бифуркации - утроению периода (цикл 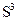). Именно эти циклы характеризуют перемежаемость: нерегулярные всплески прерываются почти периодическими колебаниями малой амплитуды, т.к. энергия колебаний в цикле 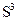намного меньше, чем в цикле 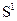. Остальные циклы 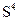, 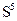и т.д. сводятся к 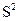и 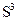. Асимметрия, неоднородность распределения амплитуд приводят к

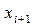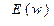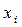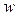Рис.2. Фазовый портрет и спектр мощности реализации, показанной на рис. 1. а)

образованию окон по вертикали. Еще одно отличие этой диаграммы от известных моделей типа бифуркации Фейгенбаума в том, что относительный интервал значений управляющего параметра на 5 и более раз больше, т.е. перемежаемость проявляется более отчетливо.

Для описания эволюции геометрических мер изменение 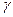ограничено до 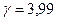. Случаи 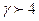описывают эволюцию меры в фазовом пространстве.

Меняя параметр 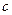при постоянном значении 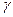мы получим аналогичную бифуркационную картину.

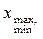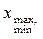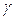
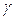а) б)

Рис. 3. Бифуркационные диаграммы отображения перемежаемости. а) 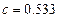, б) .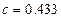

4.2. Корреляции и дисперсия сигнала не учитывают информацию о фазе, форме колебаний, т.е. они являются менее информативными, чем эволюционный параметр порядка. Этот вывод мы проверили на разных хаотических сигналах. На рис.4,5 представлены результаты обработки сигналов генератора динамического хаоса с фазовым управлением [4].

4.3. Универсальные энтропийные закономерности эволюции открытых систем к режимам самоподобия и самоаффинности согласно формулам (3.7), (3.8) представлены на рис. 6. Энтропия Шеннона нормирована на энтропию сигнала, имеющего форму равнобедренного треугольника

На рис. 7.приведены энтропийные закономерности эволюции отображений: Фейгенбаума, Хенона и отображения перемежаемости (1.13), (1.14).

Формулы отображения Фейгенбаума и Хенона:

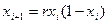, (4.1)

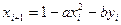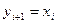, . (4.2)

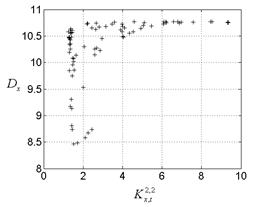
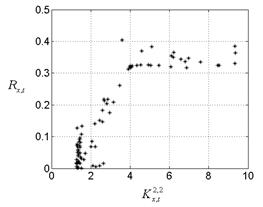
Рис. 4. Взаимозависимость корреляционных и Рис. 5. Взаимосвязь дисперсии с эволюционным

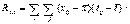эволюционных характеристик. параметром порядка.

.

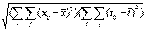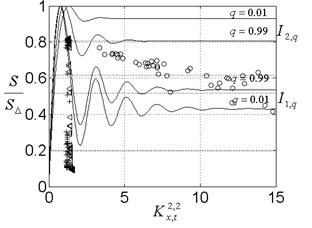В области самоорганизации попадают только те сигналы, которые соответствуют отображению, полученному в настоящей работе.

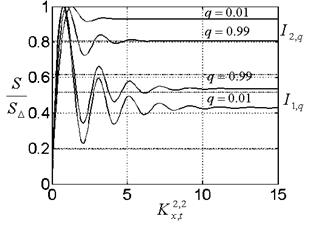
Рис. 6. Энтропийные закономерности эволюции Рис. 7. Энтропийные закономерности эволюции

открытых систем реализаций, соответствующим отображениям

Фейгенбаума (+), Хенона (∆) и формулам (1.13),

(1.14) (о).

4.4. Специфика отображения (1.13), (1.14) наглядно проявляется сравнением его реализаций с результатами численного анализа известных моделей динамических систем, в которых реализуются перемежаемость и хаос [5]:

1. Система Лоренца

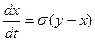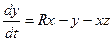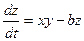, , . (4.3)

2. Система уравнений цепи Чуа

, , ,

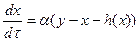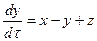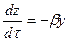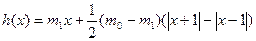. (4.4)

3. Система Ресслера

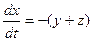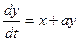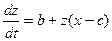, , . (4.5)

4. Генератор Анищенко – Астахова

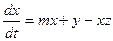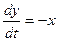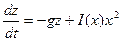, , . (4.6)

5. Генератор динамического хаоса с фазовым управлением

, , ,

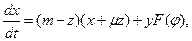
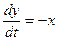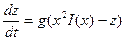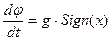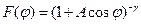. (4.7)

Генератор динамического хаоса с фазовым управлением имеет наибольшие значения эволюционного параметра порядка (рис. 8.), но база сигналов относительно мала. Отсюда следует, что для описания сложных сигналов необходимо использовать наряду с базой и эволюционный параметр порядка.

На рис. 9. приведена энтропийная закономерность эволюции всех вышеприведенных динамических систем. Видно, что только сигналы генератора динамического хаоса с фазовым управлением являются самоорганизованными при больших значениях параметра порядка.

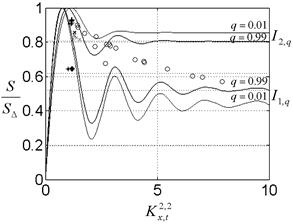
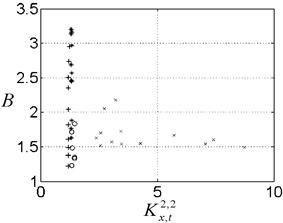
Рис. 8. База и эволюционный параметр порядка Рис. 9. Энтропийные закономерности эволюции

сигналов динамических систем: Лоренца (*) (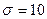, динамических систем: Лоренца (*) (,

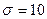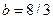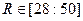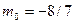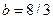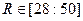, а ), Цепи Чуа (+) (, , а ), Цепи Чуа (+)

, , ), (, , ,

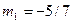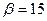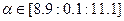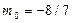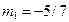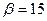Ресслера (∆) (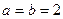 и 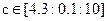), ), 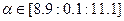Ресслера (∆)(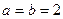

Анищенко-Астахова (о) (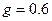, 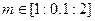), и 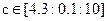), Анищенко-Астахова (х)

генератора динамического хаоса с фазовым управлением (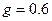, 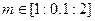) генератора

(x) (g=1.5, A=0.95, 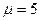, 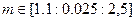). динамического хаоса с фазовым управлением

(о) (g=1.5, A=0.95, , ).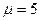

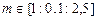Заключение

Из общих принципов - условий ограничения производной и хаотичности (скейлингового характера зависимости среднеквадратичной величины от времени) процесса получено универсальное двухпараметрическое отображение. Один из параметров имеет смысл дробной части фрактальной размерности множества значений рассматриваемой физической величины, другой – коэффициента пропорциональности в принятой скейлинговой зависимости.

Полученное отображение описывает перемежаемые, хаотические эволюционные процессы. В отличие от известных моделей данное отображение реализует перемежаемость с сильными всплесками, т.е. сигналы типа «накопление - выброс». Важно то, что именно такие сигналы удовлетворяют критериям самоорганизации. Такие сигналы ранее нами были получены теоретически, в схемотехническом, физическом экспериментах от радиотехнического генератора с фазовым управлением. Сходство реализаций имеет физическую основу. Фрактальность процесса, использованная при выводе отображения, является основным свойством самоорганизованных систем. В системе уравнений генератора динамического хаоса нами была принята нелинейная зависимость собственной частоты селективного контура от фазы обратной связи. Этот фактор тоже является одним из основных условий самоорганизации.

Предлагаемые нами универсальные закономерности эволюции открытых систем сформулированы в виде зависимости нормированной информационной энтропии от эволюционного параметра порядка. Способ нормировки энтропии, выражение эволюционного параметра порядка тоже является новыми результатами.

Список использованной литературы

1. Федер Е. Фракталы. – М.: Мир, 1991. – 254 с.

2. Zhanabaev Z.Zh. Information properties of self-organizing systems // Rep.Nat. Acad. Of Science RK. – 1996. No 5. – p. 14-19.

3. Жанабаев З.Ж. Квазиканоническое распределение Гиббса и масштабная инвариантность хаотических систем // Мат. 5-й Межд.конф. «Хаос и структ. в нелин. сист.», 15-17 июня, 2006. Астана. –Ч.1. - С. 15-23.

4. Жанабаев З.Ж., Алмасбеков Н.Е., Иманбаева А.К., Манапбаева А.Б.,

Ахтанов С.Н. Защита информации динамическим хаосом с фазовым

управлением.// Материалы 7-й международной научной конф. «Хаос и структ. В нелин. сист», 15-17 июня, 2010. Караганда. – С. 13-20.

5. Анищенко В.С. Сложные колебания в простых системах. - М.:Наука, Гл. ред. физ. мат. лит., 1990.-312 с.

АЛМАСУДЫҢ ӘМБЕБАП БЕЙНЕЛЕУІ