устройства

Последовательные корректирующие устройства получили большое распространение вследствие легкости и относительной простоты их реализации как на пассивных 4-х полюсниках, так и с помощью операционных усилителей интегрального исполнения.

Структурная схема системы с последовательным корректирующим устройством представлена на рис.7.8. В схеме приняты обоз-

Рис.7.8

начения: К_доп – дополнительный коэффициент усиления;

П(s) – передаточная функция последовательного корректирующего устройства; W_и(s) – общая передаточная функция исходной системы. Задачей синтеза последовательного корректирующего устройства является определение его передаточной функции П(s) и

К_доп . Решение этой задачи выполняется в следующем порядке:

а) по требованиям, предъявляемым к проектируемой системе строится желаемая ЛАЧХ – L_Ж (рис.7.9);

б) по параметрам элементов, входящих в исходную систему, строится её ЛАЧХ – L_И;

в) так как коэффициент усиления исходной системы, как правило, не обеспечивает требуемой точности, то по разности коэффициентов передачи (в децибелах) желаемой и исходной ЛАЧХ на рабочей частоте определяют величину К_доп в дБ (рис.7.9);

г) по передаточной функции нескорректированной системы

W_н(s) = К_доп ∙W_и(s) строится её ЛАЧХ – L_Н;

д) уточняется вид желаемой ЛАЧХ в области высоких частот. Это уточнение заключается в постепенном приближении к ЛАЧХ нескорректированной системы вплоть до пересечения и дальнейшего совпадения с ней (см.точечный пунктир желаемой ЛАЧХ между частотами ω₄ и ω₆ на рис.7.9). Еще лучше, когда высокочастотная часть желаемой ЛАЧХ с некоторой частоты (например, с частоты сопряжения ω₅ нескорректированной системы) повторяет наклоны нескорректированной ЛАЧХ, располагаясь под ней (см. жирную пунктирную асимптоту желаемой ЛАЧХ на рис.7.9). В этом случае высокочастотные помехи ослабляются, так как коэффициент передачи корректирующего устройства становится меньше единицы;

е) исходя из равенства передаточных функций

,

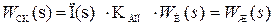определяется 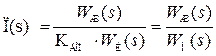; (7.20)

ж) по условиям коррекции требуется равенство коэффициентов передачи желаемой и скорректированной систем в определенном частотном диапазоне. Поэтому на основании (7.20) 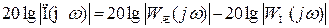строится ЛАЧХ последовательного корректирующего устройства – L_П. Построение ведется путем вычитания L_Н из L_Ж по отдельным частотным диапазонам, определяемым двумя соседними частотами сопряжения на любой из двух ЛАЧХ (L_H и L_Ж). Для наглядности процедуры представим её в форме таблицы 7.1

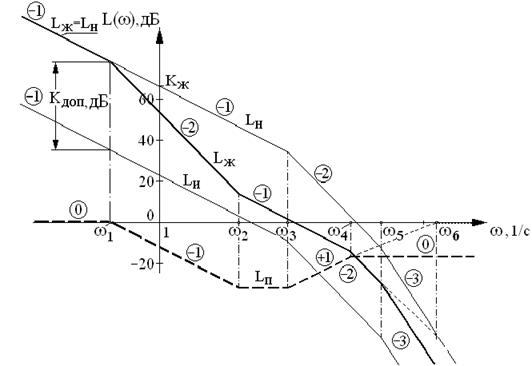
Рис.7.9

Таблица 7.1

Диапазон частот	Наклон LЖ	Наклон LН	Наклон LП (Разность наклонов LЖ– LН)
0 ≤ ω ≤ ω1	–1	–1
ω1 ≤ ω ≤ ω2	–2	–1	–1
ω 2 ≤ ω ≤ ω3	–1	–1
ω3 ≤ ω ≤ ω4	–1	–2	+1
ω4 ≤ ω ≤ ω5	–2	–2
ω5 ≤ ω ≤ ω6	–3	–3

Отметим, что вся ЛАЧХ последовательного корректирующего устройства (см. жирный пунктир) лежит в области отрицательных значений амплитуд, то есть коэффициент передачи корректирующего устройства меньше единицы.

Далее по виду ЛАЧХ записывается передаточная функция W_П(s) последовательного корректирующего устройства.

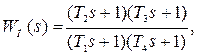
где Т₁= 1/ω₁; Т₂= 1/ω₂; Т₃= 1/ω₃; Т₁= 1/ω₁; Т₄= 1/ω₄.

(Для случая, когда ЛАЧХ последовательного корректирующего устройства в высокочастотной области продлевается до совпадения с ЛАЧХ нескорректированной системы – точечный пунктир, передаточная функция равна:

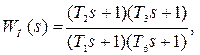где Т₆= 1/ω₆).

Электрическую схему пассивного корректирующего устройства можно узнать из справочных таблиц (4,5), фрагмент которых приведен в Приложении 4 по виду ЛАЧХ. Сопоставляя полученную ЛАЧХ корректирующего устройства с приведенной в таблице Приложения 4, выбираем схему под номером 8 или 7.

Пример 1. Для системы, функциональная схема которой дана на рис.7.10 синтезировать последовательное корректирующее устройство П(s) по следующим данным:

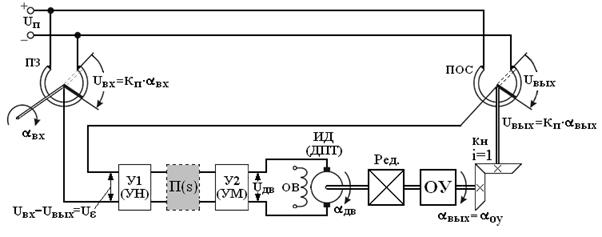
Рис.7.10

Система должна отслеживать задаваемое угловое положение объекта управления;

К_П – коэффициент передачи (крутизна) потенциометров задающе-

го и обратной связи – 3 В/рад;

К_У – общий коэффициент усиления усилителя напряжения (УН) и усилителя мощности (УМ) – 400;

К_ДВ – коэффициент передачи двигателя – 4 Рад/ В∙с;

К_Р – коэффициент передачи редуктора – 0,0015;

Т_М – постоянная времени двигателя механическая – 0,04 с;

Т_Э – постоянная времени двигателя электрическая – 0,004 с;

Т_У – постоянная времени усилителя – 0,002 с;

Максимальная скорость, развиваемая объектом управления (ОУ) – α_оу׳ = 1,75 с^–1;

Максимальное ускорение, развиваемое ОУ – α_оу״ = 0,7 с^–2;

ε_m – установившаяся ошибка при гармоническом воздействии

≤ 0,0025 рад;

σ – коэффициент перерегулирования ≤ 20 %;

t_p – время регулирования ≤ 0,2 с при допустимом отклонении равном ± 5% h(∞).

Решение. На основании функциональной схемы составим структурную схему (рис.7.11) и запишем передаточную функцию

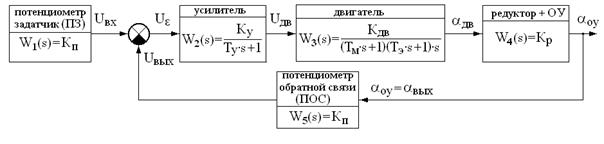
Рис. 7.11

исходной системы.

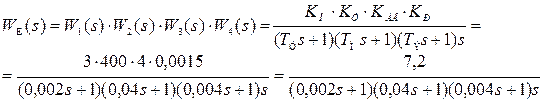(7.21)

По формулам (7.4) и (7.5) находим рабочую частоту и амплитуду эквивалентного гармонического воздействия:

;

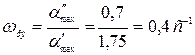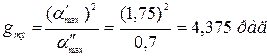
Исходя из требуемой точности воспроизведения гармонического

воздействия, определяется минимальное значение коэффициента

передачи на рабочей частоте в децибелах:

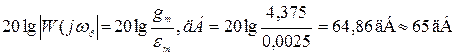
Делаем поправку на 4-ре децибела и принимаем окончательно координаты рабочей точки равными:

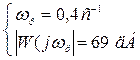(7.22)

Через точку с координатами (7.22) проводим низкочастотную аси-

мптоту с наклоном –1, поскольку исходная передаточная функция содержит одно интегрирующее звено. На частоте ω = 1 с^–1 по уравнению (7.16) низкочастотной асимптоты определяем К_Ж в децибелах:

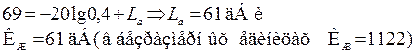
Из рабочей точки проводится асимптота с –2 наклоном до уровня амплитуды равного 12 дБ и далее – среднечастотная асимптота с наклоном –1 до уровня амплитуды равного –12 дБ. Из конца среднечастотной асимптоты в область высоких частот проводится асимптота с наклоном –2, которая после построения ЛАЧХ неско-

рректированной системы будет уточняться.

По передаточной функции исходной системы (7.21) строится ЛАЧХ – L_И (рис.7.12). Так как коэффициент усиления (К_И = 17 дБ) исходной системы не обеспечивает требуемой точности, то его необходимо увеличить до значения, равного К_Ж = 61 дБ. С этой целью применяется дополнительное усиление К_ДОП = К_Ж – К_И = = 44 дБ. Путем перемещения ЛАЧХ исходной системы параллельно самой себе по вертикали до совпадения низкочастотных асимптот L_И и L_Ж добиваемся выполнения условия по точности. Полученная ЛАЧХ обозначается L_Н и принадлежит нескорректированной системе. Эта ЛАЧХ очевидно отличается от желаемой и поэтому требуется её коррекция.

Перед тем как воспользоваться вышеизложенной методикой

следует уточнить вид желаемой ЛАЧХ в высокочастотной части.

Чтобы упростить электрическую схему корректирующего устройства и минимизировать коэффициент передачи высокочастотных помех, асимптоту с наклоном –2 на частоте сопряжения ω_Э изменяют на –3 наклон. И далее наклоны желаемой ЛАЧХ проводятся параллельно наклонам нескорректированной системы.

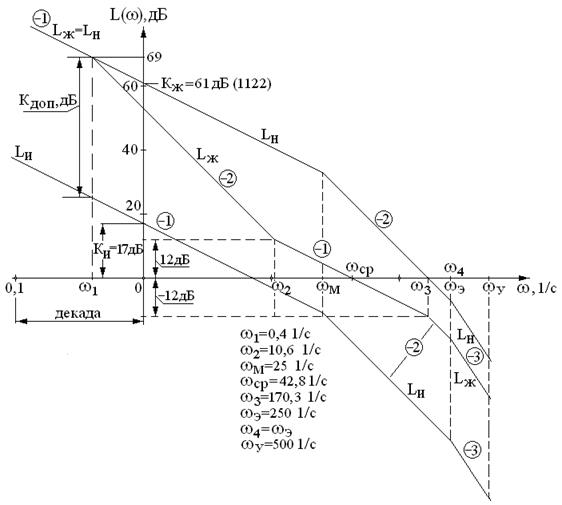
Рис.7.12

Так как последняя частота сопряжения ω_У существенно превышает частоту среза ω_СР (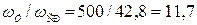), то влиянием соответствующего апериодического звена можно пренебречь. Уточненная передаточная функция желаемой ЛАЧХ будет равна:

,

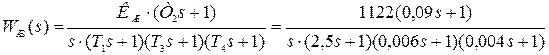где 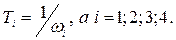Перед тем как получить ЛАЧХ корректирующего устройства следует убедиться, что желаемая система отвечает требуемым динамическим показателям. С этой целью проводится математическое моделирование. Проверка показателей качества желаемой системы нашего примера проводилась с использованием программного комплекса МВТУ и дала следующие результаты (рис.7.13). Коэффициент перерегулирования σ = 23,3%, а время регулирования t_p = 0,172 c.

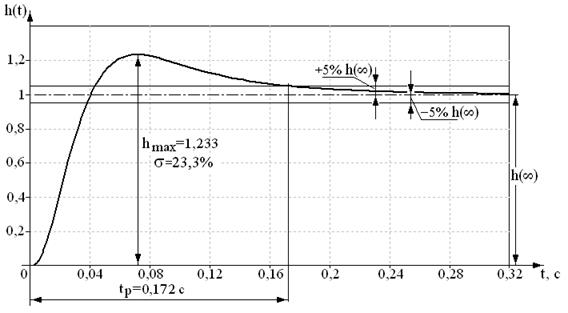
Рис. 7.13

Cформированная ЛАЧХ желаемой системы не удовлетворяет показателю перерегулирования. Так как за этот показатель отвечает протяженность среднечастотной асимптоты, то её продлим до частоты сопряжения ω_Э (рис.7.14) и считаем, что ω₃ = ω_Э.

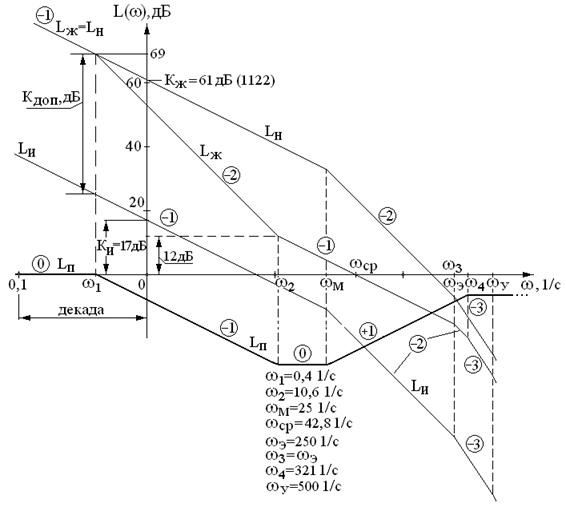
Рис.7.14

Запишем передаточную функцию уточненной желаемой ЛАЧХ, по которой проверим показатели качества:

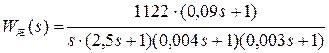(7.23)

Математическое моделирование без учета апериодического звена с частотой сопряжения ω_У дало (рис.7.15) следующие результаты: σ = 18,4% < 20 % и t_p = 0,182 c < 0,2 c.

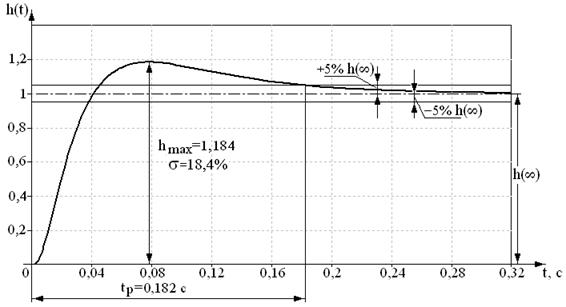
Рис.7.15

Полученные удовлетворительные результаты позволяют построить ЛАЧХ последовательного корректирующего устройства

путем вычитания L_H из L_Ж в отдельных частотных диапазонах

(см. таблицу 7.2)

Таблица 7.2

Диапазон частот	Наклон LЖ	Наклон LН	Наклон LП (Разность наклонов LЖ– LН)
0 ≤ ω ≤ ω1	–1	–1
ω1 ≤ ω ≤ ω2	–2	–1	–1
ω 2 ≤ ω ≤ ωм	–1	–1
ωм ≤ ω ≤ ω3	–1	–2	+1
ω3 ≤ ω ≤ ω4	–2	–2	+1
ω4 ≤ ω ≤ ωу	–3	–3
ωу ≤ ω ≤ ∞	–3	–3

Полученная ЛАЧХ последовательного корректирующего устройства (жирная ломаная кривая – L_П на рис.7.14) позволяет записать передаточную функцию корректирующего устройства в числовом выражении:

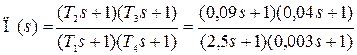, (7.24)

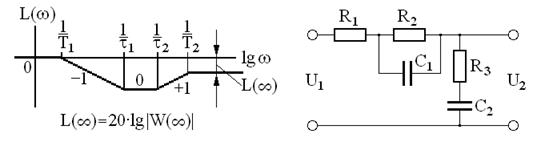
где 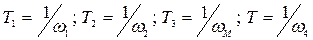, а значения частот соответствуют точкам излома ЛАЧХ корректирующего устройства. Вид ЛАЧХ (рис.7.16,а) позволяет выбрать принципиальную электрическую схему реализации (рис.7.16,б) и рассчитать параметры её резисторов и конденсаторов (см. Приложение 3 пункт 8).

а) б)

Рис7.16

Передаточная функция пассивного корректирующего устройства имеет общий вид:

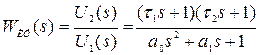, (7.25) где

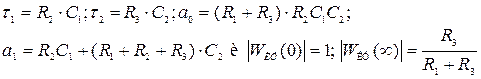
Приравнивая правые части (7.24) и (7.25), можно рассчитать параметры резисторов и конденсаторов, входящих в пассивный 4-х полюсник (рис.7.16,б)

Контрольные вопросы

1. Как выглядит структура системы с последовательным кор-

ректирующим устройством?

2. Каков порядок процедуры получения ЛАЧХ и передаточ-

ной функции последовательного корректирующего уст-

ройства?

3. В соответствие с какими принципами уточняется вид же-

лаемой ЛАЧХ в области высоких частот?

4. Чем вызывается необходимость дополнительного усиле-

ния сигнала системы и как определяется К_ДОП?

5. На какой элементной базе реализуется последовательное

корректирующее устройство?

6.Какими достоинстами обладают последовательные корре-

ктирующие устройства и какие у них недостатки?

[1] Программный комплекс «Моделирование в технических устройствах» (МВТУ) разработан в МГТУ им.Н.Э. Баумана.