Оно основано на том, что законы распределения каждой из составляющих сумму случайных величин нам неизвестны и более того, даже перечислить эти величины мы не в состоянии (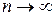 ), а поведение суммы оказывается можно предвидеть.
), а поведение суммы оказывается можно предвидеть.
Решение вопроса, при каких значениях n рекомендуется использовать нормальное приближение, зависит от требуемой точности вычисления вероятностей.
Сделаем три замечания о центральной предельной теореме, важные для практики:
Замечание 1. Если предельный вид распределения суммы случайных слагаемых при определенных условиях всегда нормален и не зависит от вида распределения самих слагаемых, то скорость сходимости распределения суммы к нормальному закону существенно зависит от типа распределения исходных компонент. Так, например, при суммировании равномерно распределенных случайных величин уже при 6-10 слагаемых можно добиться достаточной близости к нормальному закону, в то же время как для достижения той же близости при суммировании слагаемых, имеющих распределенный Хи- квадрат, понадобится более 100 слагаемых.
Замечание 2. Центральной предельной теоремой не рекомендуется пользоваться для аппроксимации вероятностей на “хвостах” распределения, т. е. при оценке вероятностей больших отклонений анализируемой суммы случайных величин от своего среднего значения. Это приводит к большим относительным ошибкам аппроксимации. Так, например, пусть 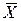 (n) – нормированный среднедушевой доход в семье (соответственно
(n) – нормированный среднедушевой доход в семье (соответственно 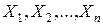 – заработная плата работающих членов семьи и другие составляющие семейного дохода) и пусть нас интересует доля q семей с очень высоким доходом, а именно с доходом, не меньшим некоторого достаточного высокого уровня
– заработная плата работающих членов семьи и другие составляющие семейного дохода) и пусть нас интересует доля q семей с очень высоким доходом, а именно с доходом, не меньшим некоторого достаточного высокого уровня 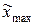 (руб.). Исследования показали, что точное значение этой доли q= 0,03, в то время как соответствующая нормальная аппроксимация дала результат
(руб.). Исследования показали, что точное значение этой доли q= 0,03, в то время как соответствующая нормальная аппроксимация дала результат 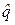 = 0,003. Разность q –
= 0,003. Разность q – 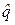 мала (как и следует из центральной предельной теоремы), однако относительная погрешность составляет величину 1000%.
мала (как и следует из центральной предельной теоремы), однако относительная погрешность составляет величину 1000%.
Особенно важным это предостережение оказывается при попытке использования нормальных аппроксимаций в задачах расчета зависимостей типа «пропускная способность» (или предельная прочность) системы – вероятность отказа в обслуживании (разрушении).
Замечание 3. Центральная предельная теорема позволяет проследить асимптотические связи, существующие между различными модельными законами распределения, с одной стороны, и нормальным законом – с другой (рис. 5.2).
Опираясь на центральную предельную теорему, можно объяснить, в частности, следующие полезные для статистической практики выводы:
1. Биномиально распределенная случайная величина X с параметрами n, p асимптотически (при 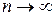 ) нормальна с параметрами M (X) = np и D (X)= np (1 – p) = npq. Данный результат известен как теорема Муавра–Лапласа (доказана впервые Муавром в 1733 г., когда еще не была известна центральная предельная теорема).
) нормальна с параметрами M (X) = np и D (X)= np (1 – p) = npq. Данный результат известен как теорема Муавра–Лапласа (доказана впервые Муавром в 1733 г., когда еще не была известна центральная предельная теорема).
2. Распределение 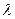 –пуассоновской случайной величины X (
–пуассоновской случайной величины X (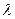 ) асимптотически (при
) асимптотически (при 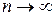 ) нормально с параметрами M (X) = D (X) =
) нормально с параметрами M (X) = D (X) = 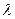 .
.
3. Другие распределения и их связи с нормальным распределением приведены на схеме (рис. 5.2).
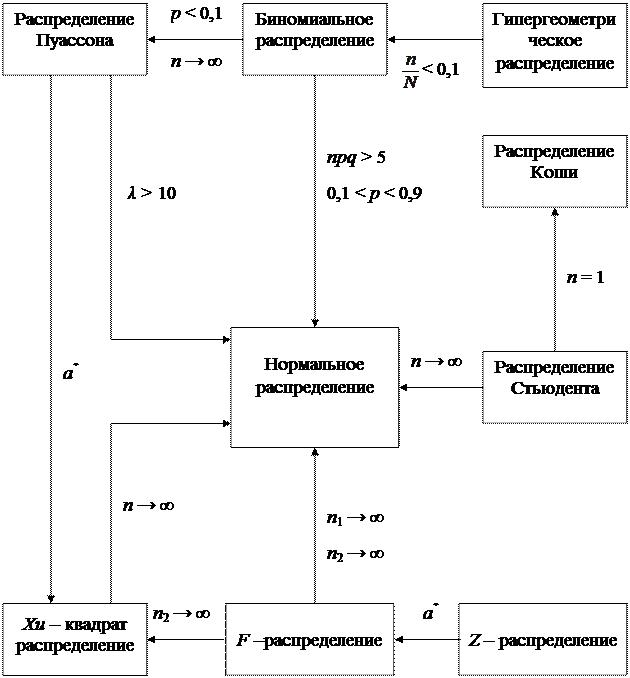
Рис. 5.2. Схема зависимостей между некоторыми распределениями;
а *– функциональное преобразование
Рассмотрим некоторые примеры практического использования центральной предельной теоремы:
1. Ошибки измерения. Случайная ошибка измерения образуется под воздействием достаточно большого числа факторов, каждый из которых вызывает как бы часть (слагаемое) суммарной ошибки. Если при этом какой-то фактор оказывает преобладающее воздействие, то и распределение суммарной ошибки будет в основном формироваться его распределением. Однако если все факторы оказываются примерно равноценными, то при достаточно большом их числе можно ожидать почти нормального распределения суммарной ошибки измерения.
2.Рассеивание при стрельбе. Известно, что при стрельбе происходит отклонение от цели точки попадания снаряда. Причиной такого отклонения является суммарное воздействие на снаряд множества факторов, например, ветра, колебания ствола орудия, неоднообразия формы и поверхности снаряда и др. В предположении относительной равноценности воздействия этих факторов и достаточно большого их числа можно ожидать почти нормального распределения суммарного отклонения.
3.Массовое производство. Пусть имеет место устойчивый технологический процесс, с помощью которого производятся некоторые изделия. Будем рассматривать в качестве случайной величины X – отклонение изготовленного изделия от стандарта, на который настроен процесс. Существует большое количество факторов, оказывающих влияние на процесс (изменение температуры, качество заготовок и т. д.). Совокупное же их действие дает уже заметный результат: изготовленные изделия имеют различные отклонения от стандарта. Из центральной предельной теоремы следует, что случайная величина X будет иметь распределение, близкое к нормальному распределению.
4. Выборочные наблюдения. Закон больших чисел и центральная предельная теорема являются теоретической основой выборочного метода, широко применяемого в статистике. Суть его состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности исследуемых объектов (ее называют генеральной совокупностью). Выборочным аналогом вероятности при большом числе наблюдений является относительная частота. Выборочное среднее арифметическое n одинаково распределенных случайных величин в случае повторной выборки удовлетворяет условиям центральной предельной теоремы и поэтому может рассматриваться как асимптотически нормально распределенная случайная величина.
Пример5.1. На распределительную базу поступило 100 одинаковых ящиков с радиолампами. M (X) числа радиоламп в каждом ящике, которые пришли в негодность за время транспортировки, равно 3, стандартное отклонение 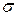 (X) = 2. Определить границы, в которых с вероятностью не менее 0,8 будет заключено общее число радиоламп, пришедших в негодность за время транспортировки.
(X) = 2. Определить границы, в которых с вероятностью не менее 0,8 будет заключено общее число радиоламп, пришедших в негодность за время транспортировки.
Решение. Пусть Y = 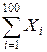 – число радиоламп, пришедших в негодность за время транспортировки. Тогда
– число радиоламп, пришедших в негодность за время транспортировки. Тогда
M (Y) = 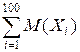 = 100×3 =300, D(Y) =
= 100×3 =300, D(Y) = 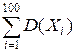 = 400.
= 400.
Воспользуемся теоремой Муавра–Лапласа
P (½ 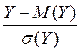 ½<
½< 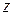 ) = 0,8;
) = 0,8;
P (M(Y) – 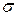 (Y) ×
(Y) × 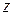 < Y < M(Y)+
< Y < M(Y)+ 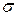 (Y) ×
(Y) × 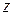 ) = 0,8.
) = 0,8.
По таблице функции Лапласа F (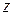 ) =
) = 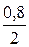 = 0,4 находим
= 0,4 находим 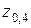 = 1,28.
= 1,28.
Тогда 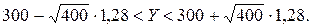
Ответ: границы, в которых заключено общее число радиоламп, пришедших в негодность, равны (300 ± 26), т. е. (274; 326).
1. В чем состоит принцип практической уверенности?
2. В чем заключается сущность закона больших чисел?
3. Чем отличается обычное понятие предела от предела по вероятности?
4. Сформулируйте и докажите теорему Чебышева.
5. Какое практическое значение имеет теорема Чебышева?
6. Сформулируйте и докажите теорему Бернулли.
7. Сформулируйте теорему Пуассона.
8. В чем особенности нормального распределения по сравнению со всеми другими распределениями?
9. В чем заключается сущность центральной предельной теоремы?
10. Приведите примеры задач, при решении которых применяется теорема Муавра–Лапласа.
Задачи
1. Вероятность того, что покупателю обуви необходимы туфли 43-го размера, равна 0,15. Оценить границы процента покупателей среди 2000 побывавших в магазине, которым нужен такой размер, если границы надо гарантировать с вероятностью 0,98.
2. Измеряется скорость ветра в данном пункте Земли. Оценить вероятность того, что скорость ветра будет выше 15 м/с, если путем многолетних измерений установлено, что среднее значение скорости ветра 6 м/с.
3. Сколько следует проверить изделий, чтобы с вероятностью, не меньшей 0,95, можно было утверждать, что абсолютная величина отклонения частоты изделий высшего сорта от вероятности изделий высшего сорта, равной 0,9, не превысит 0,01?
4. Суточный расход воды в населенном пункте является случайной величиной, среднее квадратическое отклонение которой равно 10000 л. Оценить вероятность того, что расход воды в этом пункте в течение дня отклоняется от математического ожидания по абсолютной величине более чем на 25000 л.
5. Среднесуточное потребление электроэнергии в населенном пункте равно 24000 кВт ч. Оцените вероятность того, что потребление электроэнергии в этом населенном пункте в течение данных суток превзойдет 50000 кВт ч.
6. При установившемся технологическом процессе производится 98% изделий первого и 2% второго сорта. Какова вероятность того, что среди 10000 наугад взятых изделий не более 235 окажется второго сорта?
7. Среднеквадратическое отклонение каждой из 250 000 независимых случайных величин превосходит 10. Оценить вероятность того, что абсолютная величина отклонения среднеарифметической этих случайных величин от среднеарифметической их математических ожиданий не превзойдет 0,04.
8. Норма засева зерна на 1 га равна 150 кг. Фактический расход на
1 га колеблется около этого значения. Случайные отклонения характеризуются средним квадратическим отклонением в 10 кг. Полагая, что норма высева – случайная величина, распределенная нормально, найти: а) вероятность события = {расход семян на 100 га не превысит 15,1 т}; б) массу семян, которая обеспечивает посев площади в 100 га с вероятностью 0,95.
9. Выпуск нестандартных изделий на данном производстве составляет 5%. Оценить нижнюю границу вероятности того, что в партии из 1000 изделий число нестандартных отличается от 50 не более, чем на 10.
10. Методом проб установлено, что потери зерна при уборке в среднем составляют 3 г на 1 м2; среднее квадратическое отклонение равно 1 г. Найти: а) вероятность события = {на 1 га потери составят не менее чем 29,8 кг}; б) величину, которую с вероятностью 0,99 не превысят потери на 1 га. Считать, что Х (потери зерна) есть нормально распределенная случайная величина.
11. Для некоторого автопарка среднее число автобусов, отправляемых в ремонт после месяца эксплуатации на городских линиях, равно 5. Оценить вероятность события A = {по истечении месяца в данном автопарке будет отправлено в ремонт меньше 15 автобусов}: а) если информация о дисперсии отсутствует; б) если дисперсия равна 4.
12. Дисперсия каждой из 80000 независимых случайных величин не превышает 12. Какой должна быть верхняя граница абсолютной величины отклонения среднеарифметической этих случайных величин от среднеарифметической их математических ожиданий, чтобы вероятность такого отклонения превышала 0,94?
13. В страховой компании застраховано 10000 автолюбителей. Вероятность поломки любого автомобиля в результате аварии равна 0,006. Каждый владелец застрахованного автомобиля платит в год 12 долл. страховых и в случае поломки автомобиля в результате аварии получает от компании 1000 долл. Найти вероятность: а) события A = {по истечении года работы страховая компания потерпит убыток}; б) события 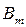 = {страховая компания получит прибыль не менее m долл.}, если m = 40000; 60000; 80000.
= {страховая компания получит прибыль не менее m долл.}, если m = 40000; 60000; 80000.
14. Случайная величина Х распределена по следующему закону
| Х | 2,2 | 2,7 | 3,0 | 3,3 | 3,5 | 3,7 | 3,9 | ||
| Р (Х = хi) | 0,05 | 0,08 | 0,2 | 0,15 | 0,1 | 0,12 | 0,1 | 0,15 | 0,05 |
Пользуясь неравенством Маркова, оценить вероятность того, что случайная величина Х примет значение, не превосходящее 3,5.
15. Среднее число вызовов на АТС за 1 минуту равно 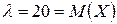 . Найти вероятности следующих событий:
. Найти вероятности следующих событий: 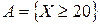 ;
; 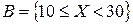 .
.
16. Произведено 600 независимых испытаний: в 250 из них вероятность появления события А была равна 0,5, в 160 – 0,7 и в 190 – 0,4. Оценить снизу вероятность того, что отклонение частоты от средней вероятности не превысит по абсолютной величине 0,04.
17. Сколько нужно произвести измерений, чтобы с вероятностью, равной 0,9973, можно было утверждать: погрешность средней арифметической результатов этих измерений не превысит 0,01, если измерение характеризуется средним квадратическим отклонением, равным 0,03?
18. Длина изготавливаемых деталей является случайной величиной, среднее значение которой 35 мм. Среднее квадратическое отклонение этой величины равно 0,15. Оцените вероятность того, что отклонение длины изготовленной детали от ее среднего значения по абсолютной величине превзойдет 0,3.
19. Рабочий изготавливает штучные изделия. Время изготовления – случайная величина, распределенная по показательному закону. Найти вероятность того, что на изготовление 100 изделий рабочему понадобится от 5 до 6 часов, если среднее время, необходимое для изготовления каждого изделия, равно 3 мин и не зависит от времени изготовления других изделий.
Литература
1. Гмурман В. Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2001.
2. Гурский Е. И. Сборник задач по теории вероятностей и математической статистике. – Мн.: Высшая школа, 1984.
3. Колемаев В. А., Староверов О. В. Теория вероятностей и математическая статистика. – М.: Наука, 1993.
4. Новротская Н. Л. Сборник задач по теории вероятностей. – Мн.: Институт управления и предпринимательства, 2005.
5. Новротская Н. Л., Петрович М. Л. Теория вероятностей. Ч. 1, 2. – Мн.: Институт управления и предпринимательства, 1997.
6. Тутубалин В. Н. Теория вероятностей. – М.: МГУ, 1972.
7. Четыркин Е. М., Калихман И. Л. Вероятность и статистика. – М.: Финансы и статистика, 1982.
 2015-07-03
2015-07-03 7419
7419
