2015-07-04
614
Гармоническая волна представляет собой бесконечную синусоиду и является фундаментальной волновой моделью. Формула волны:
.
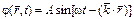
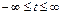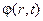‑ величина возмущения в точке с радиусом-вектором 
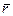в момент времени 
; 
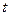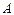‑ амплитуда возмущения; 
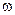‑ круговая частота 
‑ связана с периодом 
: 
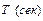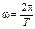, где период – время, за которое совершается один полный цикл колебаний. Часто вместо периода используется циклическая частота 
; 
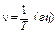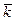‑ носит название волнового вектора. По абсолютной величине 
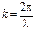равен числу волн на отрезке 
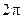и ориентирован в направлении распространения возмущения; 
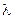‑ длина волны 
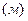‑ расстояние между двумя соседними максимумами (минимумами) возмущений. Длина волны 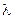и период 
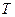связаны: 
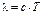, где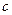 
‑ скорость распространения возмущения. Выражение, стоящее за 
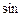в выражении волны, называют фазой: 
.
,
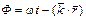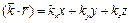если волна распространяется вдоль одной оси, например,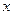 
, то
.
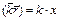Одной из характеристик волн является вид поверхностей равных фаз, т.е. поверхностей, в любой точке которых в данный момент времени фазы одинаковы. Эти поверхности называют волновыми фронтами.
|
|
|
Соответствующие волны классифицируют по виду поверхностей равных фаз: плоские, сферические, цилиндрические.
Как уже было отмечено, распространение волн связано с переносом энергии в среде от локального возмущения. Количественно он характеризуется вектором плотности потока энергии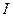 
. Направление 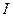совпадает с направлением переноса энергии, а его абсолютная величина равна энергии, переносимой волной за единицу времени через единичную площадь, расположенную перпендикулярно направлению потока. Обычно при расчётах используют связь потока 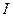и амплитуда волны 
: 
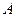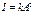, где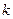 
зависит от природы волны и свойств среды.
