2015-07-04
745
Рассмотрим совокупность трёх взаимодействующих материальных точек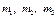 
(рис. 5). Для каждой материальной точки справедливы законы Ньютона
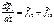
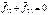
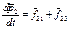
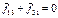
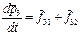
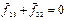
Объединим точк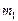и 
и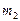 
в систему. Постулируем, что импульс системы материальных точек равен векторной сумме импульсов материальных точек, входящих в систему: 
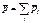. Проведём математические операции: 
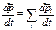. В нашем случае
.
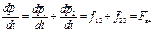Соответствующий физический закон имеет вид
.
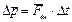В инерциальной системе отсчёта приращение импульса системы материальных точек равно импульсу приложенных к системе внешних сил.Внешние силы – силы, приложенные к системе со стороны материальных точек, не входящих в систему. Силы, действующие на материальные точки системы со стороны других материальных точек системы, называют внутренними. В данном примере силы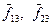 
являются внешними, силы 
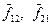‑ внутренними.
По той же схеме находят закон изменения момента импульса системы материальных точек:
.
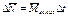Здесь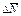 
‑ приращение момента импульса, 
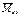‑ момент внешних сил, 
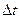‑ интервал времени, в течение которого момент внешних сил действует.
Напомним, что поскольку рассмотренный закон является следствием законов Ньютона, он справедлив в инерциальной системе отсчёта. По той же схеме находят связь между изменением кинетической энергии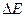 
и работой сил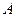 
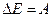. Закон работает в инерциальной системе отсчёта. Работа является суммой работ и внешних и внутренних сил. При этом внешние и внутренние силы бывают двух видов: консервативные, ‑ работа этих сил не зависит от формы пути, и неконсервативные (диссипативные), ‑ работа этих сил зависит от формы пути. Взаимное расположение материальных точек в системе называют конфигурацией. Конфигурация системы задаётся совокупностью координат материальных точек. Система может находиться в различных конфигурациях. При переводе системы из произвольной конфигурации 
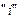в любую другую конфигурацию 
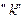меняется положение материальных точек системы, а поскольку между точками действуют силы, то производится работа 
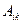. Работа есть мера передачи энергии, и если она производится за счёт внутренних консервативных сил, то определяется только разностью энергий, обусловленной взаимным расположением точек в конфигураци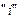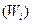и 
и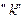 
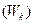. Другими словами, в этом случае 
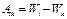. Обычно это соотношение записывают в виде: 
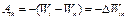. Энергию 
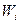, обусловленную взаимным расположением материальных точек в системе называют потенциальной. Чтобы найти потенциальную энергию конфигурации 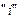, надо условно принять потенциальную энергию конфигурации 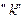равной нулю, т.е. 
.
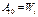Система материальных точек имеет много конфигураций. Для нахождения потенциальной энергии выбирают одну конфигурацию, имеющую нулевую энергию, и эта одна конфигурация выбирается произвольно, а значит в количественном отношении потенциальная энергия любой конфигурации определена не однозначно. Однако этот произвол не влияет на физические выводы, поскольку в физике изучаются процессы, а процесс всегда связан с изменением конфигураций и зависит не от абсолютных значений энергии, а от разности энергии различных состояний, т.е. используется формула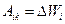 
, а она однозначна. Сумму кинетической и потенциальной энергии системы материальных точек называют полной механической энергией.
