Пусть возможные значения х находятся в интервале: -∞<x<+∞.
· Если текущая x=-∞, F(x)=p(x<X)=0; это событие - невозможное.
· Текущая x=+∞, F(x)=p(X<x)=1. Эти свойства можно записать
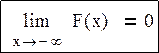
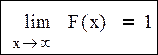
· Пусть на числовой оси выбраны две точки:
§  p(a<x<b)
p(a<x<b)
a b x
Используя определения событий можно записать: (x<b)=(x<a)+(a≤x<b) - (x<a) в данном случае событие несовместимое. По теореме сложения вероятностей p(x<b) (вероятность события, состоящего в том, что случайная величина х примет значение меньше b): p(x<b)=p(x<a)+p(a≤x<b).
p(a≤x<b)=p(x<b)-p(x<а). Можно воспользоваться определением интегральной функции. p(a<x<b)=F(a)-F(b) – вероятность того, что случайная величина попадет в заданный интервал, равна приращению ее функции распределения на этом интервале.
· F(x) не убывающая функция, то есть, если b≥a, то F(b)≥F(a).
· Вероятность того, что непрерывная случайная величина примет одно определенное значение равна нулю. Пусть a=x1, b=x1+Δx: p(x1<x<x1+Δx)=F(x1+Δx)-F(x)=0. Поэтому эквивалентны следующие записи:
- p(a<x<b)= p(a≤x<b)= p(a<x≤b)= p(a≤x≤b).
- 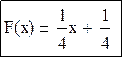 p(a≤x≤b) = p(a)+…+p(b)
p(a≤x≤b) = p(a)+…+p(b)
Построить закон распределения для, при x>0, x≤3:
p(0<x≤3)=p(0)+…+p(3)
F(x)=0, ≤0
1, >3 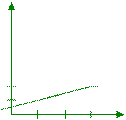
2/4
0 1 2 3
-1<x≤3
F(x)=0, x<1
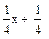 , 1<x≤3
, 1<x≤3
1, x≥3
В этом примере задана непрерывная случайная величина в виде интегральной функции, которая по определению должна быть непрерывной. Если неверно заданы границы интервалов нужно изменить их, чтобы выполнялись основные теоремы и аксиомы.
Пример, составить интегральную функцию распределения для дискретной случайной величины, обозначающей число дефектов для 3 изделий. График имеет вид ступенчатой функции, значение которой устанавливается равным сумме вероятностей возможных значений случайных величин, лежащих левее х:
x<0, F(x)=0
при 0≤x<1 F(x)=p(0)=0,125
при 1≤х<2 F(x)=p(0)+p(1)=0,5
при 2≤x<3 F(x)=p(0)+p(1)+p(2)=0,875
при x≥3 F(x)=p(0)+p(1)+p(2)+p(3)=1
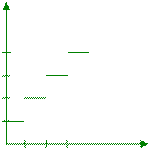 |
0,875
0,5
0,125
0 1 2 3
Таким образом, можно увидеть, что интегральный закон распределения справедлив и для непрерывных случайных величин и для дискретных случайных величин.
 2015-07-04
2015-07-04 329
329








