Три основных распределения:
· Биномиальное
· Распределение Пуассона
· Равномерное
· 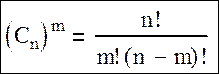 Это распределение дискретных случайных величин, где вероятность того, что случайная величина х примет значение равное некоторому значению n, определяется по формуле P(x=m)=Pn(m)=Cnm∙pm∙qn-m – это операция комбинаторики, то есть число комбинаций из n объектов по m, отличающихся только составом, определяется по формуле:
Это распределение дискретных случайных величин, где вероятность того, что случайная величина х примет значение равное некоторому значению n, определяется по формуле P(x=m)=Pn(m)=Cnm∙pm∙qn-m – это операция комбинаторики, то есть число комбинаций из n объектов по m, отличающихся только составом, определяется по формуле:
р – вероятность появления события в единичном испытании, q – вероятность непоявления события. Проведено n опытов. m меняется от 0 до значения …. Закон распределения имеет вид:
| x=m | … | m | … | n | ||
| Pn(m) | qn | npqn-1 | … | Cnm∙pm∙qn-m | … | pn |
· x=m=0
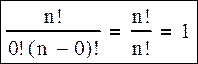
· 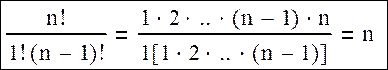 x=m=1
x=m=1
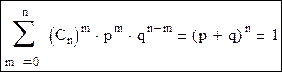 Чтобы убедиться в том, что формула Бернулли справедлива для биномиального распределения, нужно найти сумму вероятностей всех событий, указанных в таблице:
Чтобы убедиться в том, что формула Бернулли справедлива для биномиального распределения, нужно найти сумму вероятностей всех событий, указанных в таблице:
- бином Ньютона
Функция распределения:
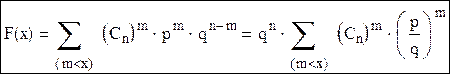
Нужно продифференцировать бином Ньютона по параметру p:
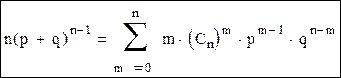
Нужно умножить обе части данного уравнения на p:
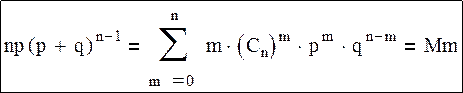
Mx=np
Дисперсия:
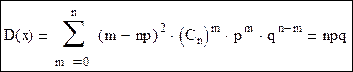
Среднее квадратическое отклонение:
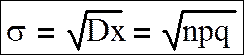
Коэффициент асимметрии:
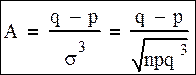
Эксцесс:
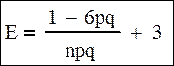
При p=q=0,5 распределение симметрично. Когда p<0,5 – асимметрия положительна, p>0,5 – отрицательная.
Форма распределения зависит не только от p, но и от n, если (n+1)p<1, то вероятность монотонно убывает с возрастанием m.
Если (n+1)p>1, то pmn имеет max при m=np
Для того чтобы убедиться в правильности формулы соответствующей биному Ньютона можно рассмотреть группу событий, возникающих при контроле двух деталей.
A – событие при m=0
B1 – при m=1
B2 – при m=2
A=B1∙B2
p(A)=p(B1)∙p(B2)=qq=q2
p2(0)=q2
A1=B1∙B2+B1∙B2
p(A1)=p(B1∙B2)+p(B1∙B2)=p(B1)∙p(B2)+p(B1)∙p(B2)
pq+qp=2pq
p2(1)=2pq
A2=B1∙B2
p(A2)=p(B1)∙p(B2)=pp=p2
p2(2)=p2
C=A1+ A2+ A3
p(C)=p(A)+p(A1)+p(A2)=q2+2pq+p2=(q+p)2=1
При больших значениях m и n сложно находить факториалы. Поэтому нужно использовать рекуррентную формулу: yi+1=φ(yi)
Для ряда вероятностей рекуррентная формула имеет вид:
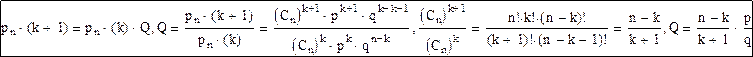
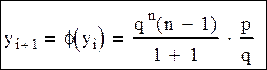
При выборе рекуррентной формулы следует учитывать начальное значение k:
k=0
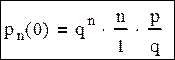
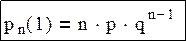
Формула справедлива при k=0. Конечное значение будет равно n-1.
Таким образом, биномиальное распределение реализует схему Бернулли, которая заключается в анализе условий повторной выборки, при которых элемент генеральной совокупности может обладать или не обладать каким-либо признаком. Вероятность одного сложного события, состоящего в том, что в n испытаниях событие наступит ровно m раз и не наступит n-m раз, по теореме умножения вероятностей pmqn-m, а всего таких событий, отличающихся только составом, Сnm.
Частным случаем является формула нахождения вероятности появления хотя бы одного из событий: A1, A2, …, An, независимых друг от друга. Она равна разности между единицей и произведением вероятностей противоположных событий: A1, A2, …, An.
p(A)=1-q1 q2 … qn
Если Ai – равновероятное, то p(A)=1-qn.
В данном случае реализуется условие повторной выборки, так как формулы для бесповторных выборок гораздо сложнее. При большом числе опытов условия повторной выборки и бесповторной практически не отличаются.
· Является предельным для биномиального распределения, если одновременно выполняются два условия:
- Число опытов бесконечно велико: n→∞, p→0.
- Вероятность события мала. Поэтому распределение Пуассона называется законом редких явлений, которые определяются как маловероятные события при значительном числе испытаний. В распределении Пуассона np=const=Q
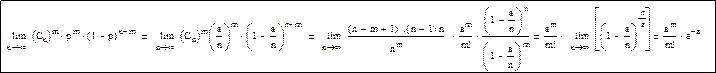
То есть формула Пуассона (1781-1840) имеет вид:
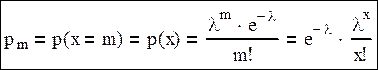
В распределении Пуассона один параметр распределения, а именно λ. Таблица закона распределения:
| x | … | n | ||
| p(x) | e-λ | e-λλ | … | 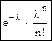
|
Функция распределения:
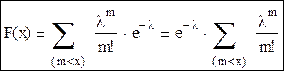
- это разложение экспоненты в ряд
Математическое ожидание:
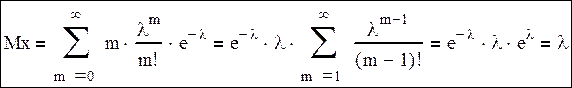
Дисперсия:
Dx=M(x2)-M2(x)=λ
Формулы показывают, что основным свойством Пуассоновского распределения является равенство математического ожидания и дисперсии.
Асимметрия:
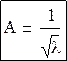
- правосторонняя
Эксцесс:
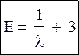
Таким образом, формула Пуассона дает хорошее приближение уже при n>20 и p<0,1.
· Равномерное (равновероятное). Все события равновероятны.
 2015-07-04
2015-07-04 1982
1982
