Центральная предельная теорема

Была сформулирована Чебышевым, а доказана Ляпуновым.

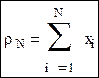Пусть имеется последовательность случайных величин x₁, x₂, …, x_n. Можно найти новую случайную величину равную сумме этих величин:

При неограниченном возрастании N закон распределения ρ_N, близок к нормальному закону. Это утверждение называется центральной предельной теоремой.

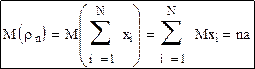
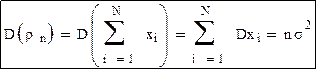Пусть x_i одинаково распределены и имеют математическое ожидание a и дисперсию σ². Тогда, используя свойства математического ожидания и дисперсии, можно найти параметры ρ_N:

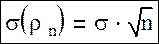
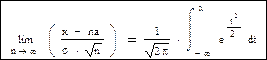Тогда в соответствии с теоремой можно записать:

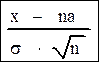
То есть случайная величина

распределена асимптотически, параллельно с математическим ожиданием равным нулю, а σ=1. x, которая равна ρ_N, имеет нормальное распределение с параметрами na и средним квадратическим отклонением σ∙√n. Физический смысл этой теоремы заключается в том, что сумма большого числа одинаковых случайных величин приближенно нормальна. При этом все слагаемые могут быть различными, но в этом случае их весовой коэффициент в сумме должен быть малым. Эту теорему наглядно подтвердил английский статистик Френсис Гальтон. Он изобрел прибор, а именно в доску, в которую были вбиты в шахматном порядке иголочки. Внизу прибора были перегородки, в которые попадали ссыпаемые в воронку.

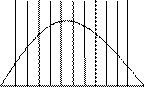
- этот прибор показал, что отклонения взаимноуравниваются, поэтому напротив воронки скапливается max количество дроби. Чтобы дробинкам отклониться далеко, нужно встретить большое число односторонних препятствий, что маловероятно. Эта теорема объясняет, почему нормальное распределение наиболее часто встречается в природе. Суммарное воздействие большого числа незначительных случайных факторов приводит к нормальнораспределенной результирующей случайной величине. Так формируется случайная ошибка, суммарная (аддитивная) помеха и так далее. На этом основан метод статистических испытаний, или метод Монте-Карло.