Доверительные границы

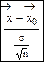
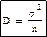
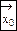
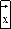Помимо рассмотренных точечных оценок статистики могут использоваться для определения интервальных оценок параметров, а значит для установления доверительных границ, внутри которых располагается значение параметра генеральной совокупности. Эти границы зависят от уровня значимости: если выборка получена в результате n независимых испытаний относительно нормально распределенной случайной величины со средним значением: 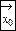и σ². Тогда выборка является совокупностью n -независимых случайных величин, распределение которых тоже нормально и имеет те же параметры распределения, а именно среднее выборки будет нормальным с математическим ожиданием 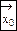и. Если σ² известна, а нет, то можно получить новую статистику, которая равна отношению отклонения среднего выборочного от его математического ожидания к основной ошибке:

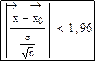. Эта статистика распределена нормально с Mx=0, σ²=1. При α=0,05 можно записать соотношение:

Ф(х)=0,96 х=1,96. Раскрыв скобки можно получить соотношение :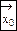

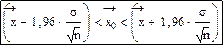
, то есть формируется интервал, который с вероятностью 0,95 будет заключать в себе среднее значение генеральной совокупности. Значения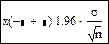

называются доверительными границами для среднего значения генеральной совокупности при 5% уровне значимости. Аналогично определяются доверительные границы при других α. Кроме рассмотренных функций и оценок существует функция: 1--β(Θ), которая называется функцией мощности критерия и выражают вероятность попадания исследуемой статистики в критическую область, если действительное значение неизвестного параметра есть Θ.

β- и γ- распределения и функции

β- и γ- функции

При оценке различных параметров, часто требуется определить те или иные статистики. Оценка этих статистик выполняется при помощи таблицы, которые в свою очередь рассчитаны для стандартных распределений, в частности: χ² -распределения, t -распределения и f -распределения. Эти распределения называются распределениями, связанными с нормальным. Формулы этих распределений содержат β - и γ - функции.

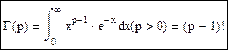γ -функция (Γ -функция) – это интеграл, выражающий факториал какого-угодно положительного числа:

- целое.

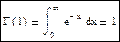Основное свойство γ -функции, называется функциональным уравнением: Γ(p+1)=pΓ(p). Рекуррентная формула:

. Г(2)=1, Г(3)=2Г(2)=2! Г(р)=(р-1)(р-2)…(р-l)Г(p-l), где l – ближайшее целое положительное число <p.

Существует теорема Роля, которая доказывает, что при одинаковых значениях функции и при второй производной Г(р)>0 (всегда больше нуля), на интервале от 1 до 2 γ -функция имеет минимум: Г(1,46163…)=0,88560.

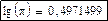При увеличении р, γ -функция резко возрастает, поэтому удобно применять таблицу логарифмов. Впервые ее получил с точностью до 12 знаков Лежандр. Есть стандартные значения: ,

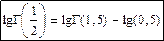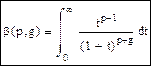γ -функция может применяться и для нахождения других неопределенных интегралов. Особенно большое значение имеет интеграл, который называется β -функцией.

β -функция:, при g=1: 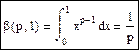, β(1,1)=0,

.

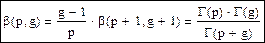
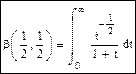Интегралы β- и γ- функций введены Эйлером и подробно исследованы Лежандром, который назвал их интегралами Эйлера первого и второго рода. Частные случаи: если p=g=1/2, то;

если t=z², то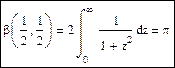

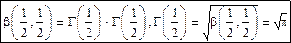
β- и γ- распределения

Распределение непрерывной случайной величины с плотностью вероятности:

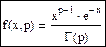
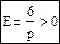называется γ -распределением. Моменты: m₁=p, m₂=p(p+1), σ²=p(p+1)-p²=p, μ₃=2p, μ₄=3p(p+2),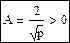

,. Если p>0, то наиболее частое значение, то есть мода достигается в точке p-1. Если p>2, то кривая касается оси абсцисс в начале координат. Если 1<p<2, то кривая касается оси ординат в начале координат. Если 0<p<1, то кривая асимптотически приближается к обеим осям.

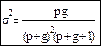β -распределение бывает первого и второго рода.

· Первого рода:

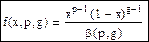
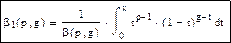
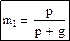, 0≤x≤1

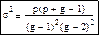
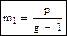
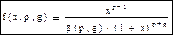· Второго рода: 0<x<∞. Моменты:

γ -распределение тесно связано с нормальным распределением. Пусть x имеет нормальное распределение с математическим ожиданием равным 0 и дисперсией σ², тогда вероятность попадания x в интервал: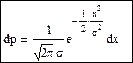

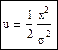
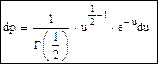
. Если x>0 или x<0, то:, где. То есть для новой статистики u, полученной из x будет характерно γ -распределение с p=1/2.

Рассмотренные распределения можно наблюдать при анализе таких распределений как: χ² -, t - и f - распределения.

χ2-распределение или распределение Пирсона

Пусть известны стандартные нормально распределенные величины: U_i=N(0,1). Распределение случайных величин: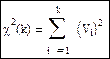

. Сумма квадратов таких величин называется χ2 -распределением с k степенями свободы. k называется параметром распределения.