На самом деле это не определение, а метод вычисления вероятностей событий во вполне определенных и сильно ограниченных условиях.
Говорят, что случайный эксперимент удовлетворяет классическому определению вероятности (или классической вероятностной схеме), если:
· пространство элементарных событий состоит из конечного числа исходов
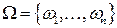 ;
;
· из соображений симметрии можно считать, что все элементарные исходы эксперимента являются равновозможными (т. е. ни один из исходов не имеет предпочтения перед другими).
Согласно классическому определению вероятности вероятность любого события 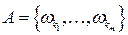 ,
, 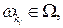
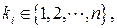
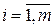 равна отношению числа исходов
равна отношению числа исходов 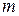 , благоприятствующих событию
, благоприятствующих событию 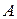 , к общему числу исходов
, к общему числу исходов 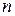 :
:
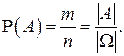
Свойства вероятности, непосредственно вытекающие из классического определения вероятности:
1°. 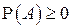 для любого события А (доказательство очевидно).
для любого события А (доказательство очевидно).
2°. 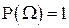 (доказательство очевидно).
(доказательство очевидно).
3°. Если события 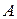 и
и 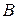 несовместны
несовместны 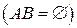 , то
, то
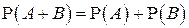 .
.
▲ Пусть событию А благоприятствует 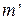 исходов, а событию В -
исходов, а событию В - 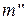 исходов. Поскольку события А и В являются несовместными (т.е. не имеют общих исходов), то сумме
исходов. Поскольку события А и В являются несовместными (т.е. не имеют общих исходов), то сумме 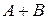 благоприятствует
благоприятствует 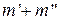 исходов. Поэтому
исходов. Поэтому
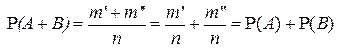 .■
.■
Исходя из свойств 1° - 3° (и только!!!) вытекают также следующие свойства вероятности:
4°. 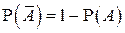 .
.
▲ Поскольку события 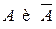 образуют полную группу событий (
образуют полную группу событий (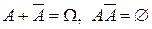 ), то из свойств 2° и 3°
), то из свойств 2° и 3° 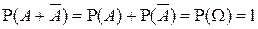 .■
.■
5°. 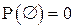 .
.
▲ Следует из свойств 2° и 4°, поскольку события 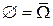 .■
.■
6°. 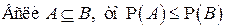 .
.
▲ Представим событие В в виде: 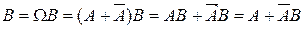 . Поскольку события
. Поскольку события 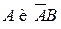 являются несовместными, то из свойств 1° и 3° имеем:
являются несовместными, то из свойств 1° и 3° имеем: 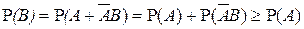 .■
.■
7°. 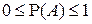 .
.
▲ Следует из свойств 2°, 5° и 6°, так как 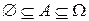 (в частности, свойство 7° означает, что измерять вероятность в процентах некорректно).■
(в частности, свойство 7° означает, что измерять вероятность в процентах некорректно).■
При решении задач с использованием классического определения вероятности, широко используются понятия комбинаторики. Напомним некоторые из них.
Размещением из N элементов некоторого множества по M элементов называется любой упорядоченный набор из M элементов данного множества. Число всех размещений равно 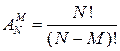 .
.
Если в упорядоченном наборе элементы могут повторяться, то этот набор называется размещением с повторениями. Число размещений с повторениями: равно 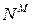 .
.
Перестановкой из N элементов некоторого множества называется размещение из N элементов по N. Число всех перестановок равно 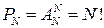 .
.
Сочетанием из N элементов некоторого множества по M элементов называется любое подмножество мощности M. Число всех сочетаний равно 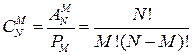 .
.
Пример 1.
Определить вероятность события А, заключающегося в том, что при бросании двух игральных костей, сумма очков не превысит 4.
Решение. В данном примере важно понимать, что если в качестве исхода эксперимента понимать значение суммы выпавших очков: 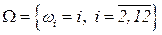 или количество очков, выпавших на каждой из костей без учета порядка их следования:
или количество очков, выпавших на каждой из костей без учета порядка их следования: 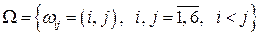 , то исходы не являются равновозможными и классическое определение вероятности не применимо. Верное решение в соответствии с классическим определением вероятности можно получить, если только под исходом понимать количество очков, выпавших на каждой из костей с учетом порядка их следования:
, то исходы не являются равновозможными и классическое определение вероятности не применимо. Верное решение в соответствии с классическим определением вероятности можно получить, если только под исходом понимать количество очков, выпавших на каждой из костей с учетом порядка их следования: 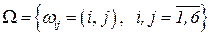 . В этом случае
. В этом случае 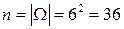 , а
, а 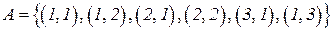 . Поэтому
. Поэтому 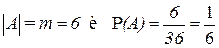 .
.
Пример 2 (Урновая схема).
В урне находится N шаров, из которых M - белые. Из урны наугад извлекается n шаров. Какова вероятность того, что среди выбранных шаров окажется ровно m белых.
Решение. Исходами в данном эксперименте являются любые подмножества, содержащие n шаров, и они являются равновозможными (за счет слова «наугад»). Число всех исходов равно числу сочетаний из N по n: 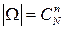 . Каждый набор шаров, входящий в интересующее нас событие, состоит из m белых шаров, которые можно выбрать из M белых
. Каждый набор шаров, входящий в интересующее нас событие, состоит из m белых шаров, которые можно выбрать из M белых 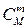 способами. Независимо от выбора белых шаров, небелые шары можно выбрать
способами. Независимо от выбора белых шаров, небелые шары можно выбрать 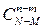 способами. Поэтому общее число благоприятных исходов равно
способами. Поэтому общее число благоприятных исходов равно 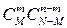 . Из этого следует, что
. Из этого следует, что 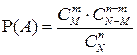 .
.
 2015-07-04
2015-07-04 908
908








