Свойства 1° – 3°, установленные в классическом, геометрическом и статистическом определениях вероятности, в аксиоматическом определении принимаются в качестве системы аксиом (только свойство 3° формулируется в более общем виде).
Определение. Пусть 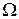 - произвольное пространство элементарных событий. Вероятностью называется числовая функция
- произвольное пространство элементарных событий. Вероятностью называется числовая функция 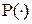 , определенная на подмножествах
, определенная на подмножествах 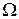 (случайных событиях), удовлетворяющая следующим аксиомам:
(случайных событиях), удовлетворяющая следующим аксиомам:
1°. Аксиома неотрицательности: 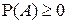 .
.
2°. Аксиома нормированности: 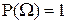 .
.
3°. Аксиома счетной аддитивности:
Для любой последовательности событий 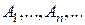 , являющихся попарно несовместными
, являющихся попарно несовместными 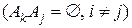
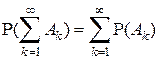 .
.
Если при изучении данного случайного эксперимента не возникает потребность в рассмотрении бесконечных последовательностей событий, то в определении вероятности аксиома счетной аддитивности 3° может быть заменена на аксиому конечной аддитивности.
3*. Аксиома конечной аддитивности: для любых событий 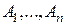 , являющихся попарно несовместными
, являющихся попарно несовместными 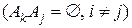
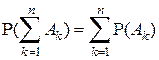 .
.
Проверка аксиомы счетной аддитивности 3° на практике бывает весьма затруднительна. Для этого полезным является следующее утверждение.
Теорема (без доказательства). Аксиома счетной аддитивности 3° эквивалентна аксиоме конечной аддитивности 3* и следующей аксиоме непрерывности:
4°. Аксиома непрерывности. Если события 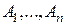 обладают свойствами:
обладают свойствами:
1) 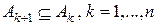 ;
;
2) 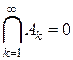 ,
,
(при этом говорят, что события образуют убывающую последовательность событий), то
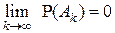 .
.
Из аксиоматического определения вероятности вытекают следующие свойства вероятности.
4°. 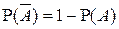 .
.
5°. 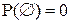 .
.
6°. 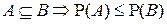 .
.
7°. 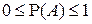 .
.
(Свойства 4° – 7° были доказаны при рассмотрении классического определения вероятности сразу в общем случае).
8°. Теорема сложения вероятностей.
Для любых событий А и В (не обязательно несовместных)
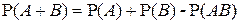 .
.
▲ Представим событие В в виде:
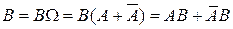 .
.
Поскольку события 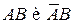 являются несовместными, то по аксиоме аддитивности 3°
являются несовместными, то по аксиоме аддитивности 3°
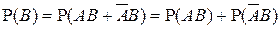 . (1)
. (1)
Представим событие 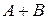 в виде:
в виде:
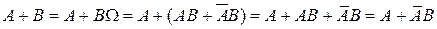 .
.
Поскольку события 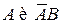 являются несовместными, то по аксиоме 3°
являются несовместными, то по аксиоме 3°
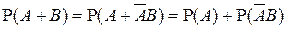 . (2)
. (2)
Вычитая из равенства (2) равенство (1), получаем
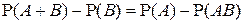 . ■
. ■
Задача. Доказать, что для любых трех событий А, В и С
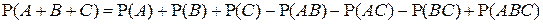 .
.
Доказать общую формулу:
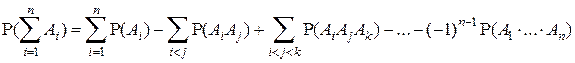 .
.
9°. Если события 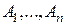 образуют полную группу событий, то
образуют полную группу событий, то
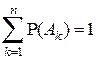 .
.
▲ Свойство следует из определения полной группы событий и аксиом 2° и 3°. ■
10°. 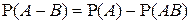 .
.
▲ Представим событие А в виде:
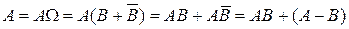 .
.
Поскольку события 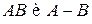 являются несовместными, то по аксиоме аддитивности 3°
являются несовместными, то по аксиоме аддитивности 3°
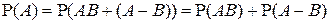 . ■
. ■
Из аксиоматического определения вероятности классическое и геометрическое определения следуют, как частные случаи (поскольку в них вероятность обладает свойствами 1° – 3°, совпадающими с аксиомами). Для примера покажем, как аксиоматическое определение вероятности позволяет конструктивно задать вероятность на любом пространстве элементарных событий, содержащем счетное число не обязательно равновозможных исходов.
Пусть 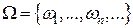 . Каждому исходу
. Каждому исходу 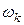 поставим в соответствие неотрицательное число
поставим в соответствие неотрицательное число 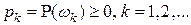 , так, чтобы
, так, чтобы 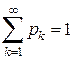 . Тогда, если вероятность любого события А определить как
. Тогда, если вероятность любого события А определить как 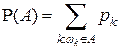 , то она будет удовлетворять аксиомам 1°, 2°, 3°.
, то она будет удовлетворять аксиомам 1°, 2°, 3°.
 2015-07-04
2015-07-04 3181
3181
