Пространство элементарных событий. Случайные события

Формализуем теперь понятие случайного события, как основополагающего понятия теории вероятностей.

Определение. Множество 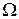всех возможных взаимоисключающих исходов случайного эксперимента называется пространством элементарных событий. Элементы множества 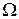называются элементарными событиями (исходами) и обозначаются w, w Î .

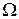Из определения следует, что при проведении эксперимента обязательно наступает одно из элементарных событий w Î 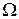. и никакие два элементарных события w₁ и w₂, отличные друг от друга, не могут наступить одновременно.

Определение. Подмножества пространства элементарных событий 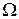, называются случайными событиями, или просто событиями.

Обозначаются случайные события прописными буквами латинского алфавита A, B, C,….

Говорят, что в результате эксперимента произошло событие 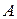, если в эксперименте произошел один из элементарных исходов, входящих в множество А.

Замечание. Вообще говоря, можно называть событиями не обязательно все подмножества 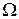, а лишь множества из некоторого набора подмножеств W, считаемых доступными наблюдению (возможными) в данном эксперименте. В случае произвольного (несчетного) 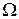такое ограничение необходимо производить для корректного определения понятия вероятности с точки зрения теории меры. Однако в данном курсе эти тонкости рассматриваться не будут (без ущерба для практических приложений) и событиями будут считаться любые подмножества .

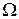Вернемся к рассмотренным в предыдущем разделе примерам с учетом введенных определений.

1. 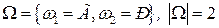, где 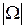- мощность множества.

2.

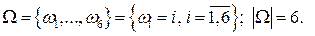
A = {Выпало четное число очков} = {2, 4, 6}.

3. .

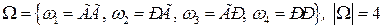A = {Выпадение герба} = .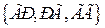

4.

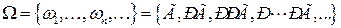
А ={Эксперимент закончится не позднее, чем на третьем шаге} =

.

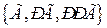5.

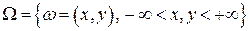
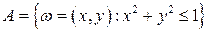= {Попадание в круг единичного радиуса}.