Условные вероятности

На практике случайные события обычно взаимосвязаны. Информация о наступлении одного из событий может влиять на шансы наступления другого. Пусть 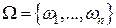- конечное пространство равновозможных исходов, А и В – некоторые события. Если о событии В ничего неизвестно, то согласно классическому определению вероятности:

.

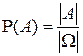Если же известно, что событие В уже произошло (т. е. наступил исход 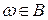, но какой именно – неизвестно), то для определения вероятности события А следует выбрать новое пространство элементарных событий .

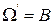В этом случае событию А благоприятствуют исходы 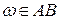и новая вероятность, которую обозначим 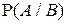, равна:

.

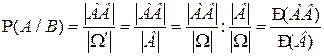Полученная вероятность называется условной вероятностью события А при условии, что событие В произошло и полученное для нее выражение в рамках классической схемы принимается за определение условной вероятности и в общем случае.

Определение. Пусть 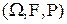- произвольное вероятностное пространство, 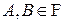- некоторые случайные события, 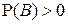. Условной вероятностью события А при условии, что событие В произошло, называется величина

.

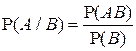Для условной вероятности 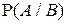применяется также обозначение .

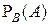Условная вероятность 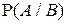, как функция события А при фиксированном событии В (условии), удовлетворяет аксиомам Р1) – Р3) и, следовательно, всем свойствам вероятности, вытекающим из аксиом:

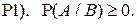
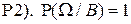
(Действительно, ).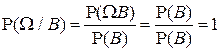

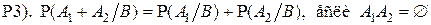
(Действительно, ,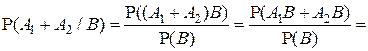

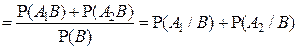поскольку события 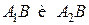являются несовместными).

Аналогично вводится понятие условной вероятности события В при условии, что событие А произошло:

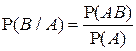
в предположении, что .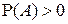

Есл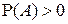и и 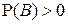, то из определения условных вероятносте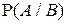й и 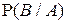получаем следующее правило умножения вероятностей:

.

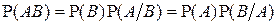На случай любого конечного числа событий правило умножения вероятностей обобщается следующим образом.

Теорема (умножения вероятностей).

Пусть 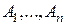- некоторые события, определенные на одном и том же вероятностном пространстве 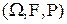, для которых 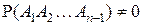. Тогда

.

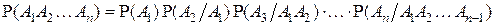▲ В соответствии с правилом умножения вероятностей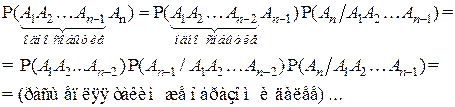

. ■

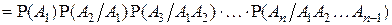Пример.

Партия из 100 деталей содержит 5 бракованных. Найти вероятность того, что среди отобранных 10 деталей не будет бракованных.

Решение. Рассмотрим события

;

.

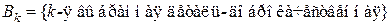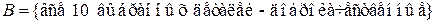Тогда 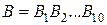и в соответствии с теоремой умножения вероятностей получаем:

.

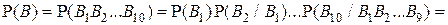
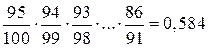Заметим, что тот же ответ получается и при использовании классического определения вероятност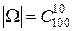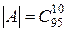и:

, и 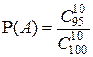= 0,584 (см. пример Урновая схема).