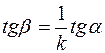Отсюда угол отражения определится из выражения

, а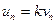

ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ШАРОВ

Удар, при котором скорости центров шаров направлены по об­щей нормали к поверхностям в точке их контакта, называют прямым центральным ударом.

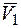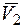Пусть два шара движутся поступательно так, что скорости их центров и направлены по прямой п-п, соединяющей эти центры и точку контакта шаров (26.8).

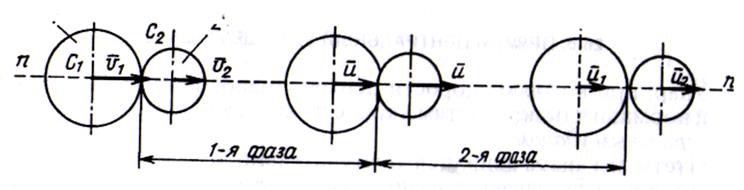
Рис. 26.8

Если v₁ > v₂, то в некоторый момент времени шары войдут в соприкосновение и произойдет удар. Если удар упругий, то шары разойдутся, имея уже скорости u₁ и U₂ .

Задача об ударе двух шаров состоит в определении скоростей шаров после удара, а также ударного импульса, исходя из заданных масс шаров т₁ и т₂, их скоростей V₁ и V_2, а также коэффициента восста­новления k.

Рассмотрим упругий удар шаров как состоящий из двух фаз. В течение первой фазы шары, имея разные скорости, входят в соприкосновение и деформируются до момента, пока их скорости не станут равными и. Во время второй фазы за счет упругих свойств шаров происходит их взаимное отталкивание, скорости шаров меняются
от общей и до различных u₁ и и₂.

Обозначим ударные импульсы за первую фазу удара через 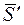, а за вторую — через 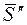. Ударный импульс, действующий на первый шар, обозначим , а на второй — 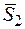. Очевидно, что ударные им­пульсы, действующие на шары, равны по модулю, противополож­ны по направлению и направлены по прямой, проходящей через центры шаров (рис. 26.9): ,

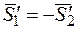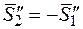
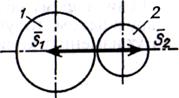
Рис.26.9

Рассмотрим первую фазу удара. Применяя теорему об из­менении количества движения системы шаров в проекции на ли­нию п-п (см. рис. 26.8), определим общую их скорость в конце этой фазы:

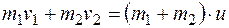
откуда 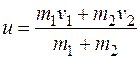. (26.26)

Ударный импульс за первую фазу найдем, применив теорему к каждому шару в отдельности:

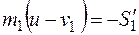(26.27)

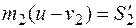
Подставляя скорость и из уравнения (26.26) в одно из написан­ных уравнений, найдем:

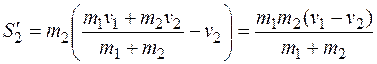
(26.28)

Рассмотрим вторую фазу удара, применив теорему об изменении количе­ства движения к каждому шару в отдельнос­ти. Имеем

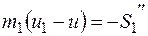
(26.29)

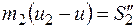
В предыдущем параграфе [см. формулу (26.19)] было показано, что коэффициент восстановления можно выразить как отношение ударных импульсов за вторую и первую фазы удара:

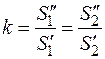
Подставим значения 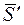и (26.29) и сократим на m₁. Получим

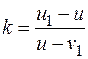(26.30)

откуда найдем скорость и₁.

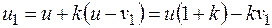(26.31)

Подставляя значение скорости и из уравнения (26.26) в уравне­ние (26.31), приводя к общему знаменателю и добавляя в числитель 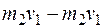окончательно получим

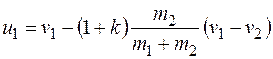(26-32)

Аналогично, подставляя в формулу (26.19) значения 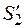и 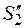из вторых уравнений систем (26.27) и (26.29), получим еще одно выра­жение коэффициента восстановления:

,

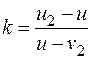из которого найдем скорость u₂:

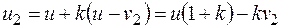(26.33)

и, подставив значение скорости и из (26.26), окончательно получим

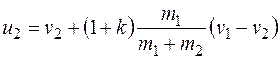(26.34)

Из выражений (26.32) и (26.34) видно, что 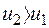. Вычитая из выражения (26.33) выражение (26.31), получим еще одну формулу для определения коэффициента восстановления:

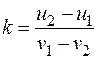(26.35)

т. е. коэффициент восстановления равен отношению взятых по мо­дулю относительных скоростей шаров.