Область определения
Если показатель степени — целое число, то можно рассматривать степенную функцию на всей числовой прямой (кроме, возможно, нуля). В общем случае степенная функция определена при 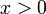 . Если
. Если 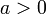 , то функция определена также и при
, то функция определена также и при 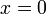 , иначе нуль является её особой точкой.
, иначе нуль является её особой точкой.
Рациональный показатель степени
§ Графики степенной функции при натуральном показателе n называются параболами порядка n. При 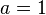 получается функция
получается функция 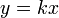 , называемая прямой пропорциональной зависимостью.
, называемая прямой пропорциональной зависимостью.
§ Графики функций вида 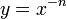 , где n — натуральное число, называются гиперболами порядка n. При
, где n — натуральное число, называются гиперболами порядка n. При 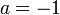 получается функция
получается функция 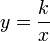 , называемая обратной пропорциональной зависимостью.
, называемая обратной пропорциональной зависимостью.
§ Если 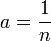 , то функция есть арифметический корень степени n.
, то функция есть арифметический корень степени n.
Пример: из третьего закона Кеплера вытекает, что период T обращения планеты вокруг Солнца связан с большой полуосью A её орбиты соотношением: 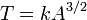 (полукубическая парабола).
(полукубическая парабола).
§ 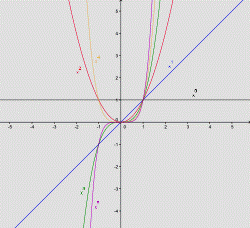
Рис. 1
Параболы порядка n: 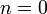 ;
; 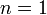 ;
; 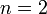 ;
; 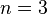 ;
; 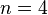 ;
; 
§ 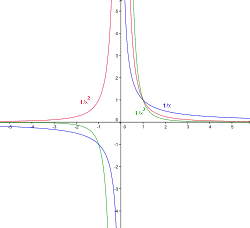
Рис. 2. Гиперболы порядка n: 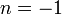 ;
; 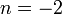 ;
; 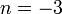
 2015-07-04
2015-07-04 386
386







