2015-07-04
425
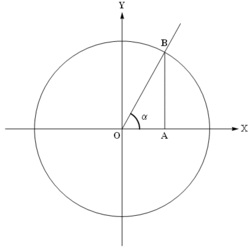
Рис. 6. Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически. Пусть нам дана декартова система координат на плоскости, и построена окружность радиуса R с центром в начале координат O. Измерим углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB.
§ Синусом называется отношение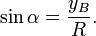 
§ Косинусом называется отношение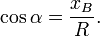 
§ Тангенс определяется как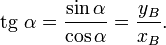 
§ Котангенс определяется как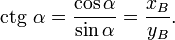 
§ Секанс определяется как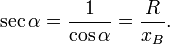 
§ Косеканс определяется как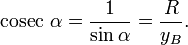 
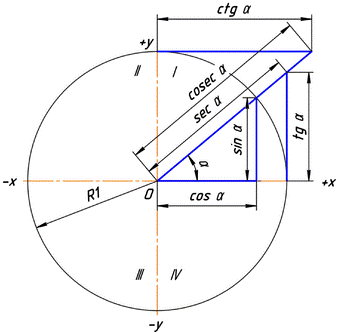
Рис. 7. Численные значения тригонометрических функций угла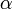 
в тригонометрической окружности с радиусом, равным единице
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB. На рисунке 7 показаны величины тригонометрических функций для единичной окружности.
Если α — вещественное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
