Десятичный логарифм

Логарифмы по основанию 10 (обозначение: 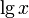) до изобретения калькуляторов широко применялись для вычислений. Они обладали преимуществом перед логарифмами с иным основанием: целую часть 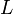логарифма числа 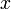легко определить.

§ Если 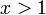, то 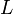на 1 меньше числа цифр в целой части числа 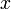. Например, сразу очевидно, что 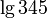находится в промежутке .

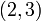§ Если 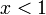, то ближайшее к 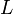целое (в меньшую сторону) равно общему числу нулей в 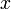перед первой ненулевой цифрой, взятому со знаком минус. Например, 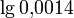находится в интервале .

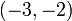Кроме того, при переносе десятичной запятой в числе на 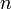разрядов значение десятичного логарифма этого числа изменяется на 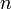. Например, 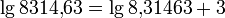. Отсюда следует, что достаточно составить таблицу десятичных логарифмов для чисел в диапазоне от 1 до 10, причём привести в таблице только мантиссы (дробную часть) логарифмов.

Связь с натуральным логарифмом:

Поскольку применение логарифмов для расчётов с появлением вычислительной техники почти прекратилось, в наши дни десятичный логарифм в значительной степени вытеснен натуральным. Он сохраняется в основном в тех математических моделях, где исторически укоренился — например, при построении логарифмических шкал.