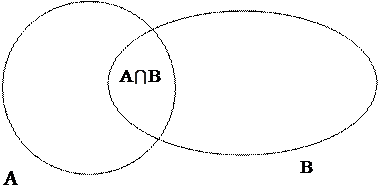ВВЕДЕНИЕ В АНАЛИЗ
Понятие множества является одним из основных первичных понятий математики. Под множеством понимается совокупность каких-либо объектов произвольной природы. Множества обозначают обычно заглавными буквами A, B, C, D, … латинского алфавита, а элементы множества – соответствующими прописными буквами - a, b, c, d, …. Задаются множества перечислением элементов или с помощью свойства, которым все элементы данного множества обладают. В последнем случае означенное свойство называют характеристическим свойством множества.
Для удобства и полноты вводится в рассмотрение пустое множество 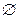 . Пустое множество не содержит элементов. Ясно, что
. Пустое множество не содержит элементов. Ясно, что 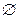 содержится в любом множестве.
содержится в любом множестве.
Часто применяемые математические обозначения.
| Символ | Как читается символ | Пример |
Символ принадлежности 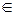
| «принадлежит», «содержится» | a 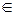 A – “a принадлежит множеству A” A – “a принадлежит множеству A”
|
Символ включения
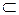
| «вложено», «содер- жится», «является подмножеством» | A 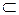 B – “множество A является подмножеством множества B” B – “множество A является подмножеством множества B”
|
Символ следования
 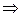
| «следует», «влечет» | 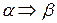 - “из предложения - “из предложения 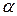 следует предложение следует предложение 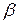 » »
|
Символ эквивалентности
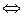
| «равносильно», «эквивалентно» | 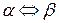 - “предложение - “предложение 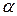 равносильно предложению равносильно предложению 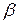 ” ”
|
Квантор всеобщности
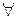
| «всякий», «любой», «произвольный», «для всех» и т.п. | см. ниже |
Квантор существования
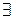
| «существует», «найдется» и т.п. | см. ниже |
| (…) | В круглые скобки помещают предложения, вытекающие из предыдущих условий | 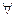 a a 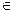 A A 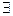 b b 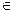 B (a B (a 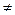 b) – “для любого элемента множества A найдется ему не равный элемент множества B” b) – “для любого элемента множества A найдется ему не равный элемент множества B”
|
Основные операции над множествами
|
|
|
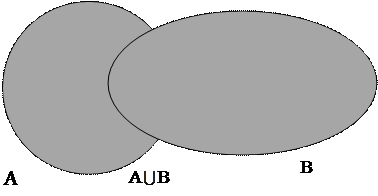
1. Объединение множеств.
Определение 1. Объединением множеств A и B называется множество, состоящее из элементов множеств A и B:
A 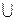 B = {c: c
B = {c: c 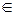 A либо c
A либо c 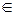 B}.
B}.
|
2. Пересечение множеств.
Определение 2. Пересечением множеств A и B называется множество, состоящее из элементов, принадлежащих как множеству A, так и множеству B:
A 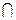 B = {c: c
B = {c: c 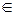 A и c
A и c 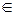 B}.
B}.
|
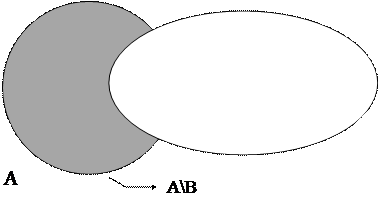
3. Разность множеств.
Определение 3. Разностью множеств A и B называется множество, состоящее из элементов множества A, не содержащихся во множестве B:
A\B = {c: c 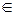 A, но c
A, но c 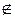 B}.
B}.
Здесь символ 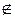 читается как “не принадлежит”.
читается как “не принадлежит”.
|
 2015-07-04
2015-07-04 1589
1589