Понятие комплексного числа
Рассмотрим выражения вида
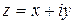 ,
,
где 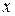 и
и 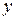 – действительные числа,
– действительные числа, 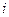 – особое число, называемое мнимой единицей. По определению
– особое число, называемое мнимой единицей. По определению
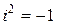 .
.
Указанные элементы будем называть комлексными числами. У комплексного числа 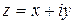 выделяют
выделяют
· 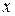 – действительную часть, пишут
– действительную часть, пишут 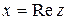 ,
,
· 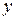 – мнимую часть, пишут
– мнимую часть, пишут 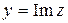 .
.
Два комплексных числа называют равными, если равны их действительные части и равны их мнимые части.
Множество комплексных чисел будем обозначать в дальнейшем 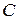 .
.
Арифметические операции
Арифметические операции над комплексными числами определяются через операции над действительными числами.
Пусть 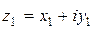 ,
, 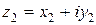 .
.
1. Сложение.
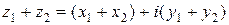
2. Умножение.
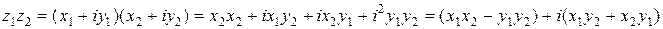
3. Вычитание.
Вычитание определяется как действие, обратное к сложению:
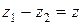 , если
, если 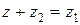 .
.
4. Деление.
Деление определяется как действие, обратное к умножению:
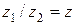 , если
, если 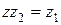 .
.
Векторная интерпретация комплексных чисел.
Модуль и аргумент комлексного числа
Каждому комплексному числу 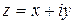 соответствует единственная упорядоченная пара действительных чисел
соответствует единственная упорядоченная пара действительных чисел 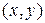 , и, наоборот, любой упорядоченной паре действительных чисел
, и, наоборот, любой упорядоченной паре действительных чисел 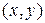 отвечает вполне определенное комплексное число
отвечает вполне определенное комплексное число 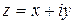 . Упорядоченные пары действительных чисел
. Упорядоченные пары действительных чисел 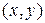 находятся во взаимно одназначном соответствии с точками (или векторами) на плоскости, на которой задана система координат. В результате комплексное число
находятся во взаимно одназначном соответствии с точками (или векторами) на плоскости, на которой задана система координат. В результате комплексное число 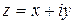 можно рассматривать как вектор на плоскости с координатами
можно рассматривать как вектор на плоскости с координатами 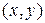 .
.
|
Координатная плоскость, векторы 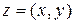 которой интерпретируются как комплексные числа, называется комплексной плоскостью, ее ось
которой интерпретируются как комплексные числа, называется комплексной плоскостью, ее ось 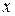 – действительной осью, а ось
– действительной осью, а ось 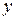 – мнимой осью.
– мнимой осью.
Длина 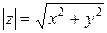
 вектора
вектора 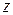 называется модулем комплексного числа.
называется модулем комплексного числа.
Если 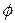 -угол между ненулевым вектором
-угол между ненулевым вектором 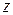 и действительной осью, то всякий угол вида
и действительной осью, то всякий угол вида 
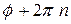 , где
, где 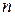 – целое число, и угол только такого вида, также будет углом, образованным вектором
– целое число, и угол только такого вида, также будет углом, образованным вектором 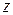 с действительной осью. Множество всех таких углов называется аргументом комплексного числа
с действительной осью. Множество всех таких углов называется аргументом комплексного числа 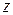 :
:
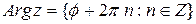 .
.
Действительная и мнимая части комплексного числа 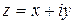 выражаются через его модуль
выражаются через его модуль 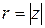 и значение
и значение 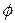 аргумента:
аргумента:
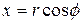
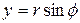 .
.
Тогда
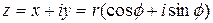 .
.
Правая часть равенства называется тригонометрической формой записи комплексного числа.
Операции с комплексными числами, записанными в тригонометрической форме
Тригонометрическая форма записи комплексных чисел удобна при перемножении чисел, возведении их в натуральную степень, при извлечении корня.
Если
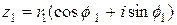 ,
, 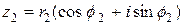 ,
,
то произведение комплексных чисел
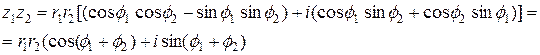
Таким образом, при умножении комплексных чисел модули перемножаются, а аргументы складываются:
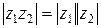 ,
,
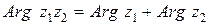 .
.
Следует обратить внимание на то, что второе равенство является равенством двух множеств.
Применив последовательно формулу умножения двух чисел к произведению 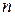 чисел, получим
чисел, получим
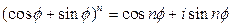 .
.
Эта формула называется формулой Муавра.
Извлечение корня из комплексного числа
Если 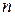 – натуральное число,
– натуральное число, 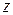 – комплексное число, то корнем n-ой степени из комплексного числа
– комплексное число, то корнем n-ой степени из комплексного числа 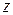 называется всякое такое число
называется всякое такое число 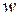 , что
, что
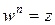 .
.
Если 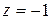 , то числа
, то числа 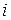 и
и 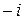 являются значениями корня 2-ой степени из –1.
являются значениями корня 2-ой степени из –1.
Следовательно, корень 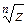 из комплексного числа
из комплексного числа 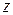 определяется неоднозначно.
определяется неоднозначно.
Корень 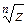 имеет ровно
имеет ровно 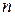 значений, вычисляемых по формуле
значений, вычисляемых по формуле
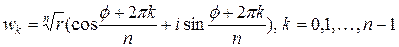 .
.
Сопряженные комплексные числа
Для каждого комплексного числа 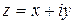 число
число 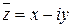 называется ему сопряженным числом. Геометрически вектор
называется ему сопряженным числом. Геометрически вектор 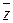 симметричен вектору
симметричен вектору 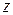 относительно действительной оси.
относительно действительной оси.
Перечислим основные свойства сопряженных чисел.
1. 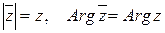
2. 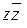
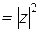
3. 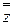
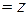
4. 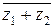
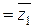
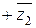
5. 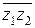
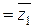
 2015-07-04
2015-07-04 1517
1517

