Понятие функции является одним из фундаментальных понятий математического анализа.
Пусть X и Y – непустые множества элементов произвольной природы.
Определение. Соответствие, при котором каждому элементу x из X отвечает единственный элемент y из Y называется функцией, заданной на множестве X со значениями на множестве Y, или отображением множества X на множество Y.
Функцию обозначают обычно буквой латинского алфавита, например, буквой 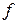 . Пишут
. Пишут
y = 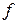 (x), x
(x), x 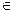 X,
X,
или
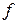 : X
: X 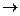 Y,
Y,
или
X 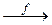 Y.
Y.
Элемент х 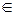 X называют независимой переменной, или аргументом, а соответствующий элемент y
X называют независимой переменной, или аргументом, а соответствующий элемент y 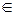 Y – зависимой переменной. Множество X называется областью определения функции, множество
Y – зависимой переменной. Множество X называется областью определения функции, множество
 Yf ={ y
Yf ={ y 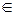 Y:
Y: 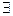 x
x 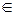 X (
X (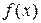 = y)}
= y)}
т.е. множество всех тех y, каждый из которых поставлен в соответствие хотя бы одному x, называется множеством значений функции. Очевидно
Yf 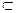 Y.
Y.
Если при 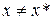 выполняется неравенство
выполняется неравенство 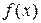
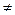
 , то функция
, то функция 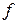 определяет взаимно однозначное соответствие X в Y.
определяет взаимно однозначное соответствие X в Y.
Если 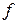 : X
: X 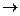 Y, E – подмножество множества X, то функция fE: E
Y, E – подмножество множества X, то функция fE: E 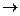 Y называется сужением функции f на множество E.
Y называется сужением функции f на множество E.
|
|
|
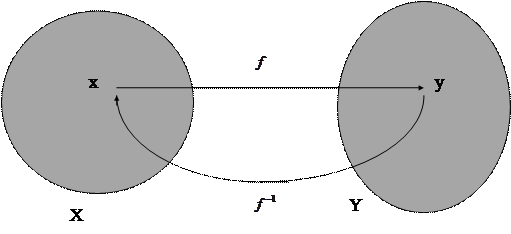
Обратная функция
Пусть 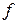 : X
: X 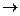 Y и для любого y из Yf найдется единственный x из X, такой, что
Y и для любого y из Yf найдется единственный x из X, такой, что 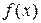 =
= 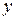 . Тогда существует обратная функция
. Тогда существует обратная функция
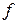 –1: Yf
–1: Yf 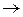 X.
X.
|
Пример. Рассмотрим функцию 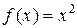 на полупрямой X={x: x
на полупрямой X={x: x 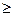 0}. Множество значений Yf = {
0}. Множество значений Yf = { 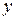 :
: 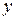
 0}, т.е. здесьY=X. Выберем произвольно
0}, т.е. здесьY=X. Выберем произвольно 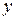
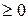 . Ему отвечает единственный
. Ему отвечает единственный 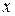 =
= 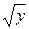 , такой, что
, такой, что 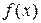 =
= 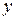 . Действительно,
. Действительно,
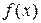 =
= 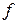 (
(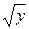 ) = (
) = (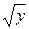 )2 =
)2 = 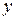 .
.
Таким образом, обратная функция здесь
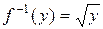 .
.
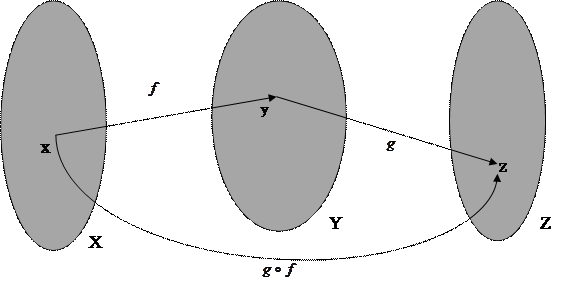
Сложная функция
Пусть 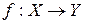 и
и 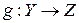 . Тогда сложная функция
. Тогда сложная функция 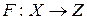 , определенная на множестве
, определенная на множестве  , ставящая в соответствие каждому
, ставящая в соответствие каждому 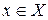 точку
точку 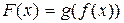 называется композицией (суперпозицией, сложной функцией) функций
называется композицией (суперпозицией, сложной функцией) функций 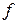 и
и 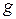 , и обозначается
, и обозначается 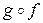 . Таким образом,
. Таким образом,
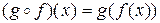
|
 2015-07-04
2015-07-04 4818
4818