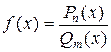Рассмотрим функции вида

,

где 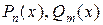– многочлены степен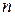и и 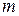соответственно.

Если степень числителя строго меньше степени знаменателя, т.е. ,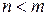

то функция 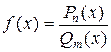называется правильной рациональной дробью, в противном случае, когда степень числителя не меньше степени знаменателя, т.е. 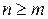, функция называется неправильной рациональной дробью.

Функция 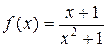есть пример правильной рациональной дроби.

Функция дает пример неправильной рациональной дроби.

Неправильная дробь раскладывается делением числителя на знаменатель в сумму:

.

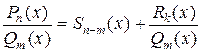Здесь 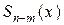– многочлен (n–m)-ой степени, называемый целой часть неправильной дроби 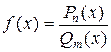, второе слагаемое 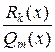есть отношение многочленов k -ой и m -ой степеней, где k<m, и называется правильной частью дроби .

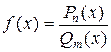Введем в рассмотрение так называемые элементарные дроби. К таковым относят дроби вида

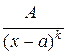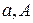1. , где – действительные числа, 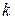– натуральное число;

2. 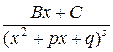, где - действительные числа, 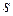- натуральное число; многочлен 2-ой степени, стоящий в знаменателе, не имеет действительных корней.

Дроби вида 1 будем называть элементарными дробями первого типа, дроби

вида 2 – элементарными дробями иторого типа.

Теорема. Правильная рациональная дробь

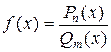
с действительными коэффициентами раскладывается в сумму элементарных дробей. При этом, если

,

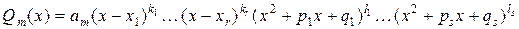где

1) 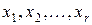- попарно различные действительные корни многочлена кратности 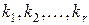соответственно,

2) многочлены второй степени не имеют действительных корней, т.е. для любого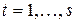

,

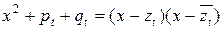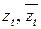- пара комплексно сопряженных корней многочлена ,

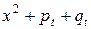3) ,

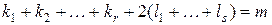то справедливо разложение

.

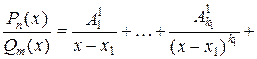
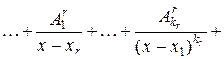
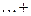
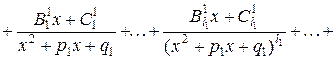
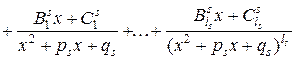Здесь 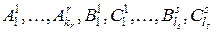- некоторые однозначно определяемые константы.

Теорема утверждает, что разложение правильной рациональной дроби определяется корнями знаменателя, причем

· действительному корню 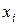кратности 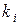, 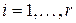отвечает серия из 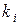элементарных дробей первого типа

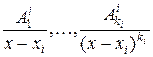
· паре комплексно сопряженных корней 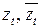, кратности 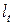, , 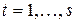отвечает серия из 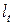элементарных дробей второго типа

.

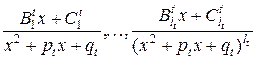Умение раскладывать правильные дроби на сумму элементарных дробей востребуется, в частности, при интегрировании функций.