2015-07-04
4184
Основное отличие краткосрочного от долгосрочного периода заключается в том, что один из ресурсов (чаще всего капитал) считается фиксированным.
- Расчет общих издержек в долгосрочном периоде:
В долгосрочном периоде меняется как труд, так и капитал. Соответственно, нам необходимо вывести функцию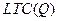 
.
Данная функция выводится следующим образом:
1) из соотношения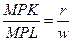 
выражается труд через капитал или капитал через труд;
2) полученное соотношение подставляется в производственную функцию, откуда получаются функции капитала и труда в зависимости от объема производства и цен на ресурсы;
3) полученные функции подставляются в уравнение издержек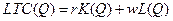 
.
Полученное таким образом соотношение и есть функция издержек в долгосрочном периоде.
Предложенный выше механизм – это, по сути, решение задачи минимизации издержек при заданном объеме производства:
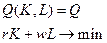
- Расчет общих издержек в краткосрочном периоде.
В краткосрочном периоде обычно капитал считается фиксированным. Функция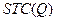 
выводится следующим образом:
|
|
|
1) из функции выпуска выражается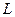 
как функция от 
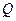при заданном объеме 
;
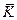2) полученная функция подставляется в уравнение издержек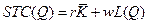 
Рассмотрим пример:
Пусть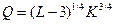 
. Цена капитала 
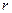, цена труда 
.
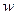- Выведем функцию долгосрочных издержек:
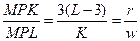
Отсюда получаем: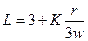 
Подставив это выражение в производственную функцию, получаем:
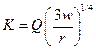и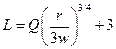 
Таким образом,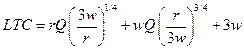 
или после преобразований получаем:
.
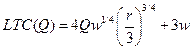- Выведем функцию краткосрочных издержек.
Пусть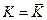 
.
Тогда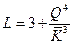 
.
.
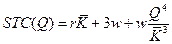Если в задаче задано конкретное значение 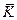, то можно его подставить сразу. Пусть 
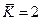, тогда 
.
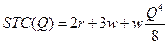Далее рассчитаем средние и предельные издержки при заданных значениях 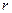и .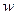
Пусть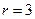 
, 
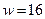, тогда:
.
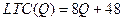
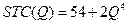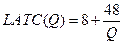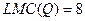
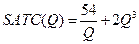и 
и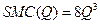 
.
Изобразим графически все 4 функции различного вида издержек.
На графике необходимо отметить следующее:
1) график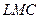 
пересечет 
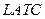в точке минимума: найдем эту точку: 
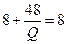. Для представленных функций уравнение решения не имеет, т.к. график средних издержек все время убывает и лежит выше графика предельных издержек:
2) график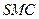 
пересечет 
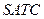в точке минимума: 
. 
. 
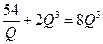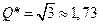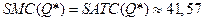(точка A на графике)
3) график 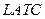есть огибающая к графикам краткосрочных средних издержек (все графики лежат выше и имеют с 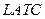точку касания), при этом в этой точке касания выполняется как равенство 
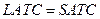, так и равенство предельных издержек 
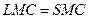. Именно из последнего соотношения и проще считать точку касания: 
, 
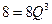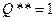(точка B). 
(точка C).
|
|
|
|
|
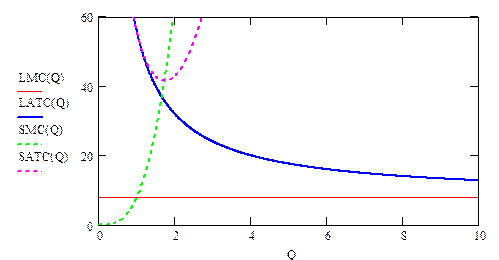
Обратите еще раз внимание, что график 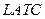касается графика 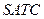, но не пересекает его!!!
Оценим эффект масштаба напрямую и с помощью индекса масштаба производства.
Оценим отдачу от масштаба напрямую:
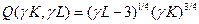
Сравним этот результат с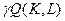 
:
|
|
|
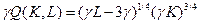
Таким образом, необходимо сравнить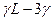 
и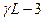 
. Т.к. 
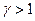(поскольку мы увеличиваем производство, а также, чтобы задача была совместима), то получаем 
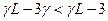, поэтому 
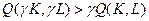, т.е. имеет место возрастающая отдача от масштаба.
Оценим отдачу от масштаба с помощью индекса масштаба. Для этого изначально рассчитаем эластичность долгосрочных издержек по выпуску:
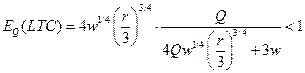, т.е. долгосрочные издержки по выпуску неэластичны!!! (если бы было больше 1, то были бы эластичны, но в контрольной такого пока не предвидится).
Таким образом, получаем, что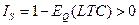 
поэтому отдача от масштаба будет возрастающей.
