 |
1. Простые проценты.
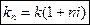 ,
,
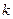 — начальная сумма,
— начальная сумма,
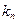 — конечная (накопленная за
— конечная (накопленная за 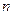 лет) сумма,
лет) сумма,
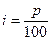 — удельная процентная ставка,
— удельная процентная ставка,
 — процентная ставка.
— процентная ставка.
Пример 6.7. Начальная сумма вклада составила 5000 ден.ед. Сколько составит накопленная сумма через три года при процентной ставке 4%?

 По условию задачи
По условию задачи 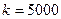 ,
, 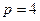 ,
, 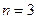 ,
, 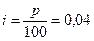 . Тогда
. Тогда 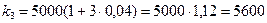 (ден.ед.).
(ден.ед.).
 2. Сложные проценты.
2. Сложные проценты.
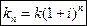 или
или 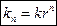 ,
,
где 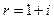 — коэффициент сложного процента.
— коэффициент сложного процента.
Пример 6.8. За период выполнения пятилетнего плана объём продукции должен возрасти на 85%. Каким должен быть средний темп роста?
 Пусть начальный объём продукции составлял
Пусть начальный объём продукции составлял 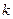 единиц. Через 5 лет он должен составить
единиц. Через 5 лет он должен составить 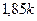 единиц (по условию задачи). С другой стороны, по формуле сложных процентов
единиц (по условию задачи). С другой стороны, по формуле сложных процентов 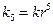 . Следовательно,
. Следовательно, 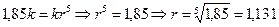 .
.
Тогда 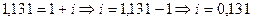 . Известно, что
. Известно, что 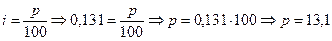 .
.
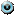 Значит для того, чтобы объём продукции за 5 лет вырос на 85%, средний темп роста должен составлять 13,1%.
Значит для того, чтобы объём продукции за 5 лет вырос на 85%, средний темп роста должен составлять 13,1%.
 |
3. Начисление процентов 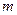 раз в году.
раз в году.

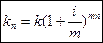 .
.
4. Периодический взнос.
В банк через определенное время (год) вносится постоянная сумма 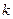 (периодический взнос) под сложные проценты при норме
(периодический взнос) под сложные проценты при норме  %. Через
%. Через 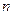 лет накопится сумма:
лет накопится сумма:
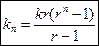 .
.
Пример 6.9. Какая сумма накопится через 10 лет, если ежегодный взнос составляет 3000 ден.ед., а ставка сложного процента 5% годовых?
 По условию задачи
По условию задачи 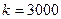 ,
, 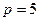 ,
, 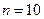 ,
, 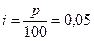 ,
,  .
.
 Тогда
Тогда 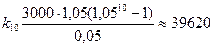 (ден.ед.).
(ден.ед.).
 5. Функция спроса.
5. Функция спроса.
При определенных условиях спрос на некоторый товар есть функция цены. Эта так называемая функция спроса. Пусть 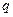 — спрос на товар,
— спрос на товар,  — цена товара. Зависимость между спросом и ценой — функция спроса — выражается формулой
— цена товара. Зависимость между спросом и ценой — функция спроса — выражается формулой
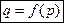 .
.
Пример 6.10. Функция спроса может иметь разный вид, например
 а)
а) 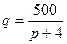 . В этом случае находим следующие соответствия:
. В этом случае находим следующие соответствия:
цена 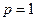 — спрос
— спрос 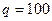 ,
,
цена 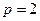 — спрос
— спрос 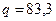 .
.
б) 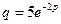 . В этом случае находим следующие соответствия:
. В этом случае находим следующие соответствия:
цена 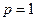 — спрос
— спрос 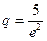 ,
,
 цена
цена 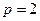 — спрос
— спрос 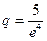 .
.
 Зависимость между спросом и ценой можно поставить двояко:
Зависимость между спросом и ценой можно поставить двояко:
1) как зависимость спроса от цены;
2) как зависимость цены от спроса.
В первом случае говорят о функции спроса, во втором о функции цен спроса; в этом случае функция есть  , а независимая переменная есть
, а независимая переменная есть 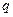 .
.
 6. Суммарная выручка.
6. Суммарная выручка.
Если количество 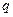 проданного товара умножить на его цену
проданного товара умножить на его цену  , получим суммарную выручку продавца или же суммарные расходы покупателя. Следовательно, суммарная выручка
, получим суммарную выручку продавца или же суммарные расходы покупателя. Следовательно, суммарная выручка
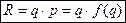 .
.
Суммарная выручка есть функция спроса. Функцией суммарной выручки называется закономерность, определяющая зависимость между суммарной выручкой и количеством проданного товара.
 Пример 6.11. Если функция цен спроса определяется посредством формулы
Пример 6.11. Если функция цен спроса определяется посредством формулы 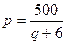 то функция суммарной выручки имеет следующий вид:
то функция суммарной выручки имеет следующий вид: 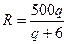 . Если
. Если 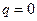 , то
, то 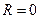 ;
;
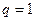 , то
, то 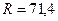 ;
;


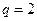 , то
, то 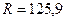 .
.
7. Функция предложения.
При прочих равных условиях предложение какого-либо товара зависит от цены. Если через  обозначить цену, а через
обозначить цену, а через 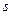 — предложение, то эту зависимость можно выразить функцией
— предложение, то эту зависимость можно выразить функцией
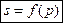 .
.
Это так называемая функция предложения.
И наоборот, каждому предложению 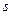 соответствует определенная цена
соответствует определенная цена  . Это можно выразить посредством зависимости
. Это можно выразить посредством зависимости
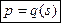 .
.
Это так называемая функция цен предложения.
 |
8. Функция средних издержек.
Закономерность, определяющая зависимость между издержками производства определенного товара и объёмом производства, называется функцией издержек. Если через 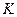 обозначить суммарные издержки производства
обозначить суммарные издержки производства 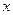 единиц продукта, то функцию суммарных издержек можно выразить в виде
единиц продукта, то функцию суммарных издержек можно выразить в виде
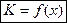 .
.
Функция 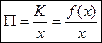 называется функцией средних или удельных издержек.
называется функцией средних или удельных издержек.
Пример 6.12. Пусть зависимость между издержками производства данного продукта и количеством произведенных единиц этого продукта имеет вид: 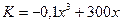 . Тогда если
. Тогда если

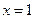 , то
, то 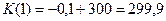 ;
;
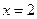 , то
, то 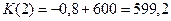 ;
;
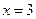 , то
, то 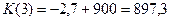 .
.
Для данного случая функции средних издержек есть
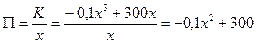 .
.
Тогда если 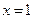 , то
, то 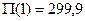 ;
;
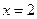 , то
, то 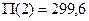 ;
;

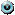
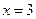 , то
, то 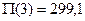 .
.
9. Распределение доходов. Итальянский экономист Парето сформулировал теорему о распределении доходов в капиталистическом обществе. Если через 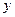 обозначить число лиц, имеющих доход, не меньше
обозначить число лиц, имеющих доход, не меньше 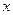 , то
, то 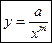 , где
, где 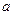 и
и 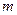 — постоянные.
— постоянные.
Закон Парето достаточно точно описывает распределение более высоких доходов; в то же время для низких доходов он не оправдывается.
Пример 6.13. Пусть в каком-либо капиталистическом обществе распределение доходов определяется уравнением 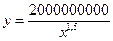 .
.
Найдите:
а) число лиц, которые обладают доходом, превышающим 100000;
б) самый низкий доход среди 100 самых богатых лиц.
 а) Имеем:
а) Имеем: 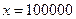 , откуда
, откуда 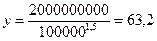 .
.
Таким образом, 63 человека имеют доход, превышающий 100000.
б) Имеем: 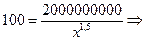
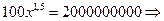
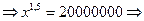
 .
.
Таким образом, самый низкий доход среди 100 богатейших лиц со 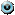 ставляет 73700.
ставляет 73700.
 § 3. Предел числовой последовательности.
§ 3. Предел числовой последовательности.
 2015-01-21
2015-01-21 396
396








