Учебно-исследовательское задание

1. Понятие статистической суммы и вывод соотношений термодинамики на его основе.

Литература

4. А.Н.Колмогоров. Три подхода к определению понятия количества информации.

5. В.Т.Горяинов, А.Г.Журавлев, В.И.Тихонов. Статистическая радиотехника. Примеры и задачи. М.: Сов.Радио, 1980.

6. Д.Д.Кловский, В.А.Шилкин. Теория передачи сигналов в задачах. М.: Связь, 1978.

Практическое занятие 13.

Тема 11: Законы распределения случайных процессов

Определения и глоссарий

Случайная величина, случайная функция времени, случайный процесс, 5 основных типов случайных процессов: дискретная последовательность, случайная последовательность, дискретный процесс, непрерывнозначный процесс, случайный поток, стационарные и нестационарные процессы, эргодические процессы

Задачи

1. Найти одномерную плотность гармонического случайного процесса 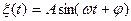с постоянными амплитудой и частотой, начальная фаза которого равномерно распределена в интервале .

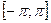2. Найти одномерную 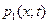и двумерную 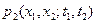плотности распределения случайного процесса 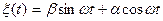, где ω - постоянная угловая частота, α и β - взаимно независимые гауссовские случайные величины с нулевыми математическими ожиданиями 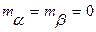и одинаковыми дисперсиями .

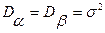3. Найти одномерную плотность распределения вероятностей процесса 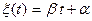, где α и β - взаимно независимые случайные величины с плотностями распределения 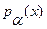и .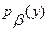

4. Найти одномерную характеристическую функцию гауссовского процесса 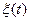, имеющего плотность распределения вероятностей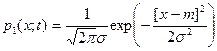

5. Пользуясь понятием условной плотности распределения и одномерной плотностью распределения гармонического процесса 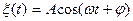с постоянной амплитудой и угловой частотой 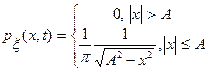, найти двумерную плотность распределения этого процесса.

6. Два гауссовских некоррелированных случайных процесса имеют заданные постоянные математические ожидания и дисперсии. Записать совместную плотность распределения вероятностей этих процессов.

7. Имеется два случайных процесса 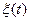и 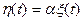, где α - постоянный коэффициент. Считая 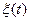гауссовским с нулевым математическим ожиданием и дисперсией 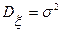, и используя определение условной вероятности, записать совместную плотность распределения 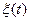и .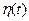

8. Определить, при каких условиях процесс 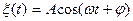, у которого амплитуда и частота - детерминированные величины, стационарен и нестационарен в широком смысле.

9. Случайные величины A и Φ независимы, 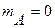, , 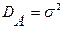Φ равномерно распределена в интервале 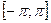. Доказать, что случайный процесс 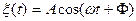стационарен в широком смысле (вычислить математическое ожидание и дисперсию процесса ).

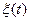10. Показать, что случайный процесс 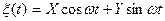стационарен в широком смысле только в том случае, когда случайные величины X и Y взаимно не коррелированы и имеют нулевые математические ожидания и равные дисперсии.