Учебно-исследовательское задание

1. Флуктуации энергии и числа частиц в термодинамических равновесных системах.

2. Зависимость термодинамических флуктуаций от времени.

Литература

1. В.И.Тихонов. Статистическая радиотехника. М.: Радио и Связь, 1982.

2. В.Т.Горяинов, А.Г.Журавлев, В.И.Тихонов. Статистическая радиотехника. Примеры и задачи. М.: Сов.Радио, 1980.

Практическое занятие 14.

Тема 12: КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ СЛУЧАЙНЫХ ПРОЦЕССОВ

Определения и глоссарий

Корреляционные и ковариационные функции случайных процессов, взаимные корреляционные функции, радиус корреляции, гауссов случайный процесс. Пуассоновский случайный процесс.

Задачи

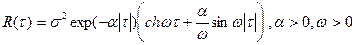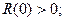
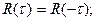
1. Определить, обладает ли функция свойствами корреляционной функци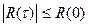и: и .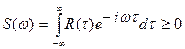

2. Случайные процессы 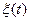и 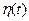заданы своими математическими ожиданиями 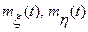, корреляционными 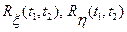и взаимными корреляционными функциями 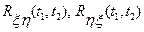. Определить математические ожидания и корреляционные функции суммы и разности этих процессов.

3. Определить корреляционную функцию 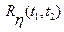случайного процесса 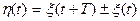, где 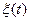- случайный процесс с нулевым математическим ожиданием и корреляционной функцией .

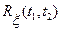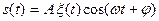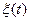4. Найти корреляционную функцию сигнала , где - стационарный случайный процесс с нулевым математическим ожиданием и корреляционной функцией 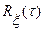, A и ω - постоянные величины, а φ - случайная начальная фаза, равномерно распределенная на интервале [-π; π] и не зависящая от .

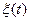5. Определить корреляционную функцию комплексного случайного процесса 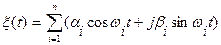, где 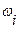- постоянная угловая частота, 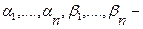взаимно не коррелированные случайные величины с нулевыми математическими ожиданиями 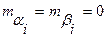и дисперсиями .

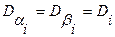6. Определить математическое ожидание 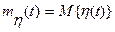и корреляционную функцию 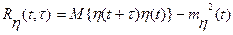периодически нестационарного случайного процесса 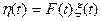, где 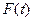- периодическая детерминированная функция, 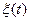- стационарный случайный процесс с математическим ожиданием 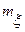и корреляционной функцией .

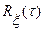7. Заданы два взаимно некоррелированных случайных процесса 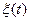и 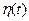с нулевыми математическими ожиданиями и корреляционными функциями 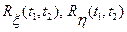. Доказать, что корреляционная функция произведения этих процессов равна произведению корреляционных функций сомножителей: .

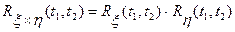8. Доказать, используя выражение для спектральной плотности, что не существует стационарного случайного процесса, корреляционная функция 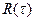которого была бы постоянна на временном интервале 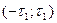и равна нулю везде вне его.

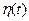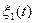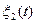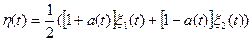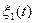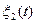9. Случайный процесс представляет собой последовательность случайно чередующихся отрезков элементарных сигналов и , т.е. имеет вид . Здесь и - стационарные и стационарно связанные случайные процессы, не зависящие от a(t), а a(t) - случайный двоичный сигнал, который в любой момент времени t может принимать одно из двух значени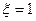й или 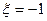с одинаковыми вероятностями 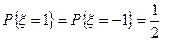, причем моменты скачков (перемен знака) распределены по закону Пуассона, т.е. вероятность обнаружения n скачков на интервале времени длительностью 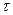определяется формулой 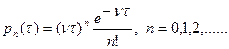Вычислить корреляционную функцию процесса 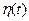при условии, что математические ожидания процессов 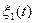и 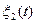равны нулю, а их корреляционные и взаимные корреляционные функции известны: 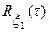, 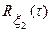и .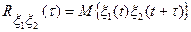

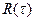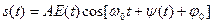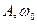10. Найти корреляционную функцию колебания , где - постоянные амплитуда и частота, 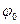- случайна начальная фаза, равномерно распределенная на интервале 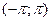, 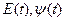- стационарные гауссовские случайные функции, медленно меняющиеся по сравнению с колебанием частоты .

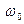11. Определить корреляционную функцию случайного процесса 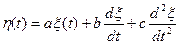, где 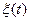- стационарный случайный процесс с нулевым математическим ожиданием и корреляционной функцией .

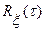12. Вычислить ковариационную функцию двоичного сигнала 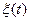, сформированного на основе простого пуассоновского потока упорядоченных временных точек 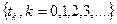следующим образом: 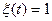, если число точек в интервале 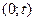- четное, 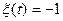, если число точек в интервале 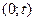- нечетное.

13. Исходя из того, что приращения простого пуассоновского потока 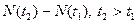на неперекрывающихся временных интервалах независимы и распределены по закону Пуассона с математическим ожиданием 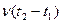, найти математическое ожидание произведения приращений на двух интервалах, когда эти интервалы не перекрываются и перекрываются.

14. Получить выражение для ковариационной функции целочисленного пуассоновского процесса .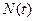

15. Вычислить математическое ожидание и ковариационную функцию приращения простого пуассоновского процесса вида 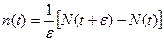, где 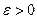- заданная величина. Изобразить график ковариационной функции и рассмотреть предел .

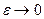16. Для простого пуассоновского процесса 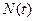вычислить одномерную характеристическую функцию.

17. Для простого пуассоновского процесса 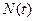при 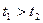и целых положительных 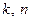вычислить вероятность .

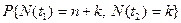18. В законе Пуассона 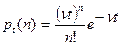длительность временного интервала 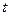является случайной величиной с плотностью 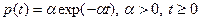. Найти вероятность появления ровно 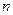событий.