Инвестиционный анализ облигаций

(1) Оценка стоимости актива и ожидаемых прибылей от владения им – один из центральных элементов инвестиционного анализа, который служит основой для принятия решений об инвестировании средств или отказа от таких намерений по отношению к конкретному объекту. Частным случаем такого анализа является оценка стоимости предприятий и их акций.

Существует много путей применения фундаментального анализа для выявления неверно оцененных бумаг. Часть из них прямо или косвенно связана с тем, что иногда называют методом капитализации дохода (capitalization of income method of valuation). Этот метод предполагает, что истинная или внутренне присущая стоимость любого капитала основана на финансовом потоке, который инвестор ожидает получить в будущем в результате обладания этим капиталом. Так как этот поток ожидается в будущем, то его величина корректируется с помощью ставки дисконтирования (discount rate), чтобы учесть не только изменение стоимости денег со временем, но также и фактор риска.

Алгебраически истинная стоимость капитала (V) равна сумме приведенных стоимостей ожидаемых поступлений и выплат:

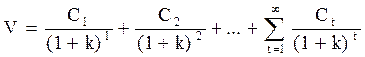(1)

где С – обозначает ожидаемое поступление или выплату, связанную с данным капиталом в момент времени t; к – соответствующая ставка дисконтирования для финансовых потоков данной степени риска. В этом равенстве ставка дисконтирования предполагается постоянной в течение всего времени. Так как знак ∞ над суммой означает бесконечность, то все ожидаемые финансовые потоки, начиная непосредственно с момента инвестирования и до бесконечности, при определении (V) будут продисконтированы с одной и той же ставкой

Так как финансовые поступления, связанные с инвестициями в те или иные виды обыкновенных акций, - это дивиденды, которые владелец акций ожидает получить в будущем, то этот способ оценивания также называют моделью дисконтирования дивидендов (dividend discount model, DDM). Соответственно вместо С_t используют D_t для обозначения ожидаемых выплат в период времени t, связанных с данной акцией, в результате равенство (1) приобретает следующий вид:

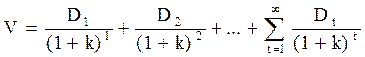(2)

Как правило, DDM используется для определения истинной стоимости одной акции той или иной компании даже в случае сделки с большим количеством акций. Тогда предполагается, что больший объем покупки можно совершить по курсу, равному произведению количества акций на цену одной акции. (Например, цена 1000 акций равна произведению 1000 на курс одной акции). Таким образом, числитель в DDM - это наличные дивиденды на одну акцию, ожидаемые в будущем.

Однако при определении истинной цены обыкновенной акции с использованием равенства (2) могут возникнуть затруднения. В частности, чтобы пользоваться этим равенством, инвестор должен предсказать все последующие дивиденды. Так как время обращения обыкновенной акции не ограничено, то необходимо прогнозировать бесконечный поток платежей. Хотя это может показаться неразрешимой задачей, при некоторых предположениях с ней можно справиться.

Данные предположения в основном связаны с темпом роста дивидендов. Пусть дивиденд на одну акцию в момент времени t равен величине дивиденда на одну акцию в момент времени t-1, умноженной на темп роста дивидендов g_t.

D_t=D_t-1(1+g_t) (3)

Что эквивалентно:

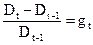(4)

Например, если в момент времени t=2 ожидаемый дивиденд на одну акцию равен $4, а дивиденды на одну акцию в момент времени t=3 составляют $4,20, то g=($4,20-$4)/$4=5%.

Применяемые методы дисконтирования дивидендов различаются в зависимости от предположений о темпе роста дивидендов и обсуждаются далее. Мы начнем с простейшего случая модели нулевого роста.

Модель нулевого роста.

Одно из предположений относительно роста дивиденда в будущем состоит в том, что размер дивидендов остается неизменным. То есть величина дивидендов на одну акцию, выплаченная за прошедший год, будет также выплачена и в следующем году и т. д.:

D₀=D₁=D₂=…=D_∞ (5)

Это тождественно предположению, что темп роста дивидендов равен нулю, так как если g_t=0, то в равенстве (3) D_t=D_t-1. Поэтому такая модель часто называется моделью нулевого роста (zero-growth model). Таким образом, стоимость акции будет находиться по следующей формуле:

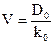(6)

Пример.

В качестве примера использования DDM предположим, что компания Zinc обещает выплачивать дивиденды в размере $8 на акцию в течение неопределенного периода в будущем при требуемой ставке доходности 10%. С помощью равенства (6) можно увидеть, что курс акции компании равен $80 ($8/0,10). При текущем курсе акции $65 следует, что NPV одной акции составляет $15 ($80 - $65). Иначе говоря, так как V= $80 > Р = $65, то акция недооценена на $15 и является кандидатом на приобретение.

Модель постоянного роста.

Другая рассматриваемая разновидность DDM – это модель, в которой предполагается, что дивиденды будут расти от периода к периоду в одной пропорции, т.е. с одинаковым темпом роста. Такую модель иногда называют моделью постоянного роста (constantgrowth model). Предполагается, что дивиденды на одну акцию, выплаченные за предыдущий год D₀ вырастут в данной пропорции g так, что в следующем году ожидаются выплаты в размере D₀(l + g). Через год после следующего ожидается, что дивиденды вырастут в той же самой пропорции g, т.е. D₂=D₁(1+g). Так как D₁=D₀(1+g), то это эквивалентно следующему: D₂=D₀(1+g)², или в общем виде:

D_t=D₀(1+g)^t (7)

Таким образом, модель оценки акций с постоянным ростом будет выглядеть следующим образом:

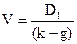(8)

Пример. В качестве примера того, как может использоваться эта разновидность DDM, предположим, что за прошедший год компания Cooper выплатила дивиденды в размере $1,80 на акцию. Прогнозируется, что дивиденды по акциям компании Cooper будут расти на 5% каждый год в течение неопределенного срока. Ожидаемые дивиденды за следующий год составят $1,89 ($1,80х(1+0,05)). Предполагая, что требуемая ставка доходности к равна 11%, можно увидеть, что курс акции компании равен $31,50 [$1,80х(1+0,05)/(0,11-0,05)= $1,89/(0,11-0,05)]. При текущем курсе акции $40 будет следовать, что NPV одной акции составляет -$8,50 ($31,50-$40). Или иначе: так как V= $31,50 < Р = $40, то акция переоценена на $8,50 и является кандидатом на продажу.

Модель переменного роста.

Более общей разновидностью DDM для оценки обыкновенных акций является модель переменного роста (multiple-growth model). Главная особенность данной модели – это период времени в будущем (обозначаемый через Т), после которого ожидается, что дивиденды будут расти с постоянным темпом g. Инвестору приходится заниматься прогнозом дивидендов до периода Т, однако при этом не предполагается, что до этого времени они будут изменяться по какому-то определенному закону. Лишь после наступления периода Т предполагается, что размер дивидендов меняется с постоянным темпом роста. Иначе говоря, вплоть до времени Т для каждого периода инвестор делает индивидуальный прогноз по величине дивидендов – D₁, D₂, D₃...D_T. Инвестор также прогнозирует наступление момента Т. Предполагается, что после наступления момента времени T дивиденды будут расти с постоянным темпом g, что означает:

D_T+1=D_T(1+g) (9)

Таким образом, формула модели переменного роста оценки акций будет выглядеть следующим образом:

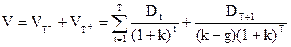(10)

Пример. В качестве примера того, как может использоваться данная разновидность DDM, предположим, что компания Magnesium выплачивала дивиденды в размере $0,75 на акцию. В следующем году ожидается, что Magnesium будет выплачивать дивиденд в размере $2 на акцию. Таким образом, g₁=(D₁-D₀)/D₀=($2-$0,75)/$0,75=167%. Через год дивиденд ожидается в размере $3 на акцию и, следовательно, g₂=(D₂-D₁)/D₁=($3-$2)/$2=50%. Начиная с этого момента времени, имеется прогноз, что в будущем величина дивидендов будет расти с постоянным темпом 10% в год, т.е. T = 2 и g = 10%. Таким образом, D_T+1=D₃=$3(1+0,1)= $3,30. При значении требуемой ставки доходности по акциям компании Magnesium в 15% величины V_T^- и V_T⁺ будут составлять $4,01 и $49,91 соответственно, а их сумма равна $53,92. Таким образом, текущий курс акции $55 оказывается справедливым. Иначе говоря, акции компании Magnesium оценены примерно правильно, поскольку разница между V и P невелика.

(2) Эмитент облигации – самая важная характеристика облигации. Именно эмитент определяет степень рискованности облигации, и именно эта характеристика часто служит определяющей при подборе аналитиком. Действительно, когда вы даете в долг деньги кому-то, вам очень важно знать, кому именно, т.к. исходя из этого вы сразу оцените потенциальный риск невозврата.

Приоритет облигаций обуславливает важность держателя в случае ликвидации эмитента. По очевидным причинам, данная характеристика облигаций относится лишь к корпоративным облигациям (т.е. предполагаем, что государство никогда не обанкротится).

В случае дефолта, компания обязана выплатить долги держателям облигаций и кредиторам, а потом уже, если что-то останется, - часть от владения акционерам. Иными словами, держатели облигаций стоят первые в списке получения своих денег в случае если компания обанкротится. Но и среди этого первого эшелона есть первые и вторые. Таким образом, по приоритету, облигации делятся на:

· преимущественные

· субординированные

Преимущественные облигации гарантируют держателю, что он будет в списке первых, кто получит свои деньги при ликвидации предприятия.

Собурдинированные облигации, наоборот, дают держателю больше прибыли в обмен на то, что средства свои держатель получит во втором эшелоне после преимущественных облигаций в случае ликвидации эмитента.

Большинство покупателей облигаций обращают большое внимание на рейтинги агентств, поскольку они влияют не только на возможную реакцию рынка, но и на сравнительную величину рыночной доходности. Облигации, имеющие рейтинг от ВВВ до ААА называют облигациями «инвестиционного класса». Те облигации, которые имеют более низкий рейтинг, называют «спекулятивными». «Бросовые» облигации (junk bonds) или высокодоходные представляет собой в высшей степени спекулятивные ценные бумаги, обладающие низким рейтингом. Многие инвесторы находят эти облигации достаточно привлекательными, поскольку они обеспечивают весьма высокую доходность (16 % и выше). Между тем высокая доходность обеспечивалась только благодаря высокой степени риска, которую влекла за собой покупка таких облигаций. Таким образом, чем ниже рейтинг, тем выше доходность облигаций.

Таблица 1. – Рейтинг облигаций.

Аaa	ААА	Высококачественные инвестиционные облигации. Самый высокий рейтинг; степень вероятности выплаты номинала и процентная ставка очень высока
Аa	АА	Высококачественные инвестиционные облигации. Высокое качество по всем стандартам, но курс несколько ниже, так как понижена степень надежности.
А	А	Инвестиционные облигации среднего качества. Имеют много хороших инвестиционных свойств, но чувствительны к неблагоприятным изменениям в экономике
Вbb	ВВВ	Инвестиционные облигации среднего качества. По этим облигациям выплачиваются номиналы и проценты, но они слабо защищены от влияния неблагоприятных экономических условий.
Вb	ВB	Спекулятивные выпуски. Имеют среднюю степень защиты номинала и процентов в разные экономические периоды.
В	В	Спекулятивные выпуски. Обычно не имеют хороших инвестиционных свойств. Вероятность выплаты номинала и процентов невелика
Саа	ССС	Высокорискованные облигации. Низкокачественные выпуски, обязательства по которым или не выполняются, или существует опасность их невыполнения.
Са	СС	Высокорискованные облигации. Высокоспекулятивные выпуски, обязательства по которым часто не выполняются. Обладают также другими рыночными недостатками.
С	.	Высокорискованные облигации. Такие выпуски считаются почти не имеющими инвестиционных качеств.
.	C	Высокорискованные облигации. Это рейтинг доходных облигаций, по которым не выплачиваются проценты.
.	D	Высокорискованные облигации. Обязательства по этим выпускам фактически не выполняются; проценты и суммы погашения депонированы эмитентом.

Ценность облигации, как и любого другого актива, определяется приведенной стоимостью ожидаемого денежного потока. Следовательно, нужно найти приведенную стоимость аннуитета и единовременно выплачиваемой величины номинала. Формула для расчёта оценки облигации выглядит следующим образом:

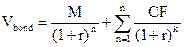(11)

V_bond - текущая цена облигации;

CF - годовой купонный доход;

r - требуемая норма прибыли;

n - число лет до погашения облигации;

M - нарицательная стоимость, выплачиваемая при погашении облигации.

Пример. Номинал облигации 10 000 рублей, доход по облигации 17% (требуемая норма прибыли), номинальный доход 14% (годовой купонный доход), срок погашения 8 лет. Оцените стоимость облигации.

14% номинальный доход соответствует ежегодным процентным выплатам в размере 1 400 рублей
V_bond = 1400 / (1 + 0,17) + 1400 / (1 + 0,17)² + 1400 / (1 + 0,17)³ + … + 1400 / (1 + 0,17)⁸ + + 10000 / (1 + 0,17)⁸ = 8737 рублей.

Структура процентных ставок.

Чем больше риск, что облигация останется неоплаченной, тем больше премия за риск неплатежа. Одно это может заставить эмитентов облигации с более высоким риском неплатежа предлагать более высокую доходность к погашению. Если к тому же верно, что чем больше риск неплатежа имеет облигация, тем больше ее премия за риск, то обещанная доходность к погашению должна быть еще выше. В результате облигации, получившие более низкие рейтинговые оценки, должны иметь более высокую обещанную доходность к погашению, в том случае если такие рейтинги действительно отражают риск неплатежа.

Если бы абсолютный уровень риска определялся принадлежностью к определенной классификационной группе по рейтингу, то каждая такая группа была бы связана с определенной вероятностью неплатежа (или, более точно, с набором вероятностей неплатежа). Следовательно, поскольку экономическая ситуация становится более неопределенной при ее анализе посредством таких показателей, как краткосрочный уровень валового национального продукта, то облигации должны были бы переклассифицироваться с продвижением, в основном на более низкие уровни. В этом случае разброс процентных ставок между отдельными группами менялся бы очень слабо, так как каждая такая группа продолжала бы отражать облигации, имеющие ту же самую вероятность неплатежа. Однако этот разброс меняется с течением времени. Это наблюдение можно интерпретировать как подтверждение того, что рейтинговые группы не отражают абсолютных уровней риска.

Известно, что рейтинговые агентства предпочитают избегать многочисленных изменений рейтингов по мере усиления неопределенности экономической ситуации. Вместо этого они предпочитают использовать классификации для определения относительного уровня риска. Это означает, что всеобщий рост нестабильности в экономике не будет приводить к значительному количеству пересмотров классификаций. Таким образом, вероятность неуплаты по облигациям в данной рейтинговой группе должна быть в такое время больше. Наоборот, спреды доходности между различными группами корпоративных облигаций и между корпоративными и государственными облигациями должны увеличиваться. И действительно, наблюдения подтверждают, что спред между обещанными доходностями облигаций для разных рейтинговых групп увеличивается, когда растет степень нестабильности экономики в целом.

Фьючерсные ставки и цены на облигации.

Рассмотрим взаимосвязь фьючерсной цены и соответствующей облигации, допущенной к поставке.

Трейдер, желающий приобрести облигации в будущем, может либо купить фьючерсный контракт сегодня, уплатив только часть стоимости, а именно дополнительную маржу, либо приобрести сегодня облигацию на спот рынке и держать ее. В последнем случае возникает необходимость произвести затраты в виде полной стоимости облигации, однако, они могут быть возмещены получением купонного дохода. С другой стороны, фьючерсная позиция не требует ни финансовых затрат, ни наличия реальных длинных спот-позиций на рынке.

Следовательно, для поддержания на рынке равновесия цена фьючерса должна определяться так, чтобы покупка фьючерсов и непосредственно облигаций приводила к одинаковому результату. Теоретически должно быть невозможно провести безрисковую прибыльную операцию на спот и срочном рынке (проведение таких операций называется арбитраж). Ниже приводится сравнение этих двух инвестиционных стратегий.

Таблица 2. – Инвестиционные стратегии с использованием фьючерсов и облигаций.

Время	Период	Приобретение фьючерса: инвестиции/стоимость	Покупка облигации на спот рынке: Инвестиции/стоимость
Сегодня		Открытие фьючерсной позиции (никаких денежных затрат)	Приобретение облигации (рыночная цена плюс НКД)
	Период обращения фьючерса	Инвестирование сэкономленных свободных средств на денежном рынке	Получение купона (если имеется) и инвестирование соответствующей суммы на денежном рынке
Время поставки		Стоимость портфеля: Облигации (приобретенные по цене фьючерса) + доход от инвестиций	Стоимость портфеля: Стоимость облигации включая НКД + все полученные купоны + все проценты, полученные на сумму инвестированных купонов

Цена фьючерса может быть либо ниже, либо выше, чем цена базового актива. Это зависит от того, являются ли затраты на поддержание позиции положительными или отрицательными. Базис убывает при приближении срока исполнения. Этот эффект называется «сходимость базиса» и может быть объяснен тем фактом, что при уменьшении оставшегося времени обращения фьючерса, снижается как стоимость фондирования, так и доход от облигаций. В день исполнения базис равен нулю. Таким образом, цену фьючерса можно считать эквивалентом цены базового инструмента. Сходимость базиса (схематически) представлена на рисунке 1.

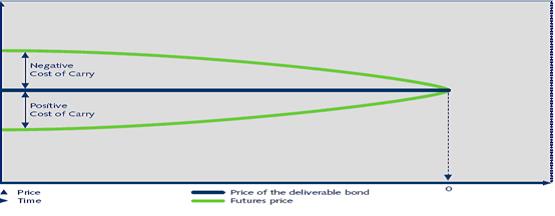
Рисунок 1. – Сходимость базиса.

Можно проследить следующую зависимость:

- Стоимость фондирования > Доход от спот-позиции: – > Затраты на поддержание позиции отрицательны;

- Стоимость фондирования < Доход от спот-позиции: – > Затраты на поддержание позиции положительны.