2015-07-04
34670
Если даны две точки плоскост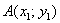и 
и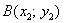 
, то вектор 
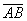имеет следующие координаты:
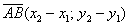
Если даны две точки пространства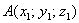 
и 
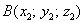, то вектор 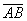имеет следующие координаты:
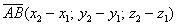
То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора.
Задание: Для тех же точек запишите формулы нахождения координат вектора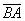 
. Формулы в конце урока.
Пример 1
Даны две точки плоскост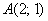и 
и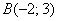 
. Найти координаты вектора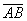
Решение: по соответствующей формуле:
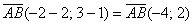
Как вариант, можно было использовать следующую запись:
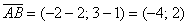
Эстеты решат и так: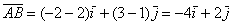 
Лично я привык к первой версии записи.
Ответ: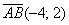 
По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения некоторых моментов чайникам, не поленюсь:
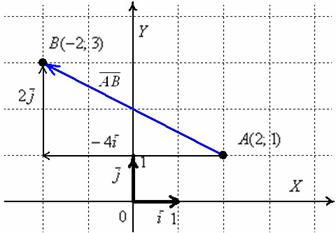
Обязательно нужно понимать различие между координатами точек и координатами векторов:
Координаты точек – это обычные координаты в прямоугольной системе координат. Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.
Координаты же вектора – это его разложение по базису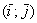 
, в данном случае 
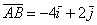. Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости .
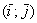Записи координат точек и координат векторов вроде бы схожи: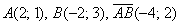 
, а смысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства.
Дамы и господа, набиваем руку:
Пример 2
а) Даны точки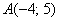 
и 
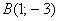. Найти векторы 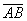и .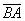
б) Даны точки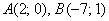 
и 
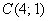. Найти векторы 
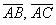и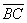 
.
в) Даны точки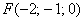 
и 
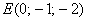. Найти векторы 
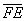и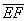 
.
г) Даны точки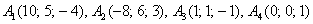 
. Найти векторы 
.
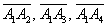Пожалуй, достаточно. Это примеры для самостоятельного решения, постарайтесь ими не пренебрегать, окупится;-). Чертежи делать не нужно. Решения и ответы в конце урока.
Что важно при решении задач аналитической геометрии? Важно быть ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫМ, чтобы не допустить мастерскую ошибку «два плюс два равно нулю». Сразу извиняюсь, если где ошибся =)
