Если 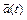 и
и 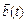 дифференцируемые вектор-функции,
дифференцируемые вектор-функции, 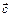 - постоянный вектор,
- постоянный вектор, 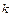 - постоянный скаляр,
- постоянный скаляр, 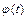 - скалярная функция, то:
- скалярная функция, то:
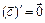
| 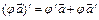
|
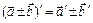
| 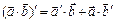
|
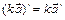
| 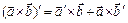
|
Уравнение касательной к пространственной кривой 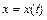 ,
, 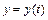 ,
, 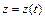 в точке
в точке 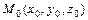 , которой соответствует значение параметра
, которой соответствует значение параметра 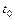 , имеет вид:
, имеет вид: 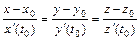 , а уравнение нормальной плоскости в той же точке – вид:
, а уравнение нормальной плоскости в той же точке – вид:
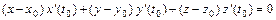 .
.
Кривизной кривой в точке 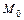 называется число
называется число 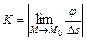 , где
, где 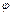 - угол поворота касательной, соответствующий дуге
- угол поворота касательной, соответствующий дуге 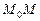 данной кривой, а
данной кривой, а 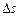 - длина этой дуги.
- длина этой дуги.
Кривизна 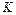 плоской кривой вычисляется по формуле
плоской кривой вычисляется по формуле 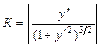 и по формуле
и по формуле 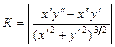 , если кривая задана в параметрическом виде уравнениями
, если кривая задана в параметрическом виде уравнениями 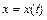 ,
, 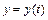 .
.
Величина 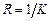 называется радиусом кривизны.
называется радиусом кривизны.
5.346. Найти единичный касательный вектор годографа вектор-функции 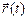 при
при 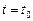 :
:
а) 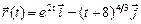 ,
, 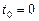 ; б)
; б) 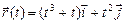 ,
, 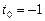 .
.
5.347. Найти производные вектор-функций 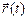 :
:
а) 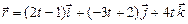 ; б)
; б) 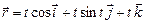 ;
;
в) 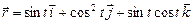 ; г)
; г) 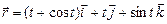 .
.
5.348. Найти производные вектор-функций 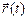 при
при 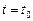 :
:
а) 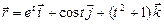 ,
, 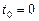 ;
;
б) 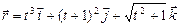 ,
, 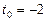 .
.
5.349. Для каждой из следующих кривых написать уравнения касательной и нормальной плоскости в данной точке:
а) 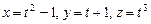 при
при 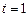 ;
;
б) 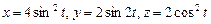 при
при 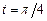 .
.
5.350. Вычислить радиус кривизны кривых в данной точке:
а) 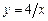 ,
, 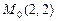 ; б)
; б) 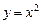 ,
, 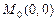 ;
;
в) 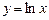 ,
, 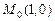 ; г)
; г) 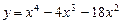 ,
, 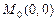 ;
;
д) 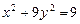 ,
, 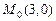 ; е)
; е) 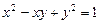 ,
, 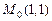 .
.
5.351. Вычислить радиус кривизны кривых в данной точке:
а) 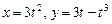 ,
, 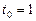 ; б)
; б) 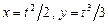 ,
, 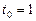 ;
;
в) 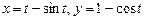 ,
, 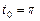 ; г)
; г) 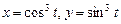 ,
, 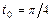
 2015-03-20
2015-03-20 557
557








