Глава 1. Системы линейных уравнений и арифметическое векторное пространство

А Л Г Е Б Р А

(1 часть)

Тирасполь 2002г.

Составители: канд. педагогических наук, доцент кафедры алгебры и геометрии Ермакова Г.Н., старший преподаватель кафедры математического анализа и методики преподавания математики Драганов А.В.

Рекомендовано к кафедральному изданию заседанием Научно-методического совета ПГУ им.Т.Г.Шевченко 03.04.02г. протокол №8.

Рецензенты: Ю.М. Рябухин, доктор физико-математических наук, академик АНМ;

А.Д. Герасимова, кандидат педагогических наук, доцент кафедры математического анализа и методики преподавания математики ПГУ

Настоящий задачник-практикум предназначен для студентов первого курса физико-математического факультета Является пособием для самостоятельного овладения методами и способами решения задач по разделам: «Системы линейных уравнений и арифметическое векторное пространство», «Матрицы и определители», «Комплексные числа», - в объёме действующей программы курса алгебры. Пособие содержит теорию (обзорно), образцы решения задач, задачи для самостоятельного решения.

Глава 1. Системы линейных уравнений и арифметическое векторное пространство.

§1. Системы линейных уравнений и их решение методом Гаусса.

Линейное уравнение. Вид противоречиво линейного уравнения. Общий вид cистемы линейных уравнений. Множество решений. Равносильные сис­темы. Следствие системы. Элементарные преобразования системы линейных уравнений. Метод Гаусса решения систем линейных уравнений. Распределение неизвестных на главные и свободные.

В общем виде линейное уравнение (уравнение первой степени) запи­шется в виде:

a₁ x ₁+a₂ x ₂+...+a_n x _n=b, (1)

где a₁,a₂,...,a_n,b – фиксированные числа (коэффициенты при неизвестных и свободных член). Не исключается случай, когда уравнение имеет вид:

0× x ₁+0× x ₂+...+0× x _n=b. (2)

Решением уравнения (1) называется любой упорядоченный набор (l₁,l₂,...,l_n) (вектор g =(l₁,l₂,...,l_n)) чисел l₁,l₂,,...,l_n, таких, что при подстановке их вместо соответствующих неизвестных уравнение обращается в верное чис­ловое равенство

a₁ l ₁+a₂ l ₂+...+a_n l _n=b.

Очевидно, что при b =0 уравнению (2) удовлетворяет любой набор значений неизвестных, а при b ¹0 не удовлетворяет ни один набор значений. При b =0 уравнение (2) назовем тождественным, а при b 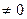– противоречи­вым.

Если даны m линейных уравнений с неизвестными x₁, x₂, ..., x_n и требу­ется найти общие решения всех уравнений, то в этом случае говорят о сис­теме m линейных уравнений с n неизвестными (система S). Такую систему записывают в виде:

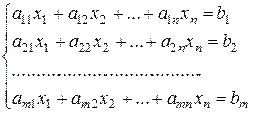
(3)

Решением системы (3) называется упорядоченный набор (l₁,l₂,...,l_n) (вектор g=(l₁,l₂,...,l_n)) чисел l₁,l₂,...,l_n.

Cистема называется совместной, если она имеет хотя бы одно реше­ние, и несовместной, если она не имеет ни одного решения.

Для любой системы возможны только три случая:

1. система несовместна;

2. система имеет единственное решение (совместно определенная);

3. система имеет бесчисленное множество решений (совместно неопре­деленная).

Промежуточный случай, когда решений конечное число, притом больше чем одно, невозможен.

Система S₂ называется следствием системы S₁, если всякое решение системы S₁ является решением системы S₂ или если S₁ несовместна.

Понятно, что всякая часть линейной системы, в том числе и одно от­дельно взятое уравнение, будет ее следствием.

Две линейные системы называются равносильными, если каждая из них является следствием другой, т.e. системы равносильны, если множества их решений совпадают.

В процессе решения системы проводятся такие ее преобразования, ко­торые не изменяют множества решений. В частности система заменяется равносильной при выполнении элементарных преобразований, к которым относятся:

1. перестановка двух уравнений системы;

2. вычеркивание уравнения вида 0 х ₁+0 х ₂+…+0 x _n=q;

3. умножение какого-либо уравнения системы на число, отличное от нуля;

4. прибавление к одному уравнению системы другого ее уравнения, умноженного на некоторое число.

Универсальным методом решения линейных систем является метод по­следовательного исключения неизвестных (метод Гаусса).

Рассмотрим систему (3). Если она содержит уравнение вида (2) и b ≠0, то множество решений пусто. Процесс решения на этом закончен. Если в уравнении (2) b =0, то его можно удалить из системы, не изменяя множества решений. Поэтому можно считать, что в каждом уравнении исходной сис­темы хотя бы один из коэффициентов при неизвестных отличен от нуля. Пусть а ₁₁≠0 (в противном случае поменяем местами уравнения или перену­меруем неизвестные). Исключим теперь x ₁ из всех уравнений, начиная со второго. Для этого ко второму уравнению прибавим первое, умноженное на –а₂₁/ а₁₁, затем к третьему уравнению прибавим первое, умноженное на
–а₃₁/а₁₁, и т.д, к последнему уравнению прибавим первое, умноженное на
– а _m1/ a ₁₁. В результате этой серии элементарных преобразований получим сис­тему:

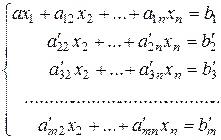(4)
равносильную исходной. Удалим из системы (4) нулевые уравнения (в связи с этим, в процесcе решения системы число уравнений может уменьшиться). Если хотя бы одно из уравнений системы (4) является противоречивым, то эта система и, следовательно, исходная несовместны.

Далее предположим, что 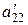¹0, и продолжим процесс исключения неиз­вестных. Поскольку число таких шагов не превышает n (числа неиз­вестных), после конечного числа преобразований получим систему вида
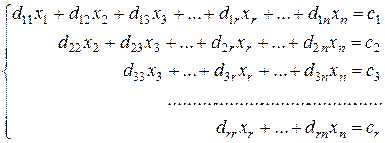(5)
(где «диагональные» коэффициенты d₁₁, d₂₂,d₃₃,…, d_rr, r£n, отличны от нуля), равносильную исходной системе (3).

Если r=n (в этом случае говорят, что система (5) имеет треугольный вид), то из последнего уравнения находим значение неизвестной x_n: x_n=c_n/d_nn. Подставив значение x_n в предпоследнее уравнение, получим значе­ние неизвестной x_n–1 и т.д., т.е. идя снизу в верх, найдем значения всех неизвестных.

Итак, в случае r=n решение системы (5) (а значит, и (3)) единст­венно.

Если r<n (в этом случае говорят, что система (5) имеет вид трапе­ции), то неизвестные x₁,x₂,…,x_r (их называют главными) можно выразить через x_r+1,x_r+2,…, x_n. Неизвестные x_r+1,x_r+2,…,x_n называют свободными, так как, выбрав произвольным образом их значения x_r+1=l_r+1, x_r+2=l_r+2,… x_n=l_n, одно­значно находим значения главных неизвестных x₁=l₁,x₂=l₂,…,x_r=l_r кото­рые в совокупности дают решение (l₁,l₂,…,l_r,l_r+1,…,l_n) исходной системы уравнений. Любое решение системы (3) можно получить таким образом. Сис­тему, в ко­торой главные неизвестные выражены через свободные, можно рас­сматривать как общее решение исходной системы, т.е. как характеристиче­ское свойство множества ее решений.

Таким образом, в случае r<n система имеет бесконечное множество решений.

Итог сказанному можно подвести с помощью следующей теоремы.

Теорема. Если система линейных уравнений совместна, то с помощью элементарных преобразований ее можно привести к системе (5) с неравными нулю коэффициентами d₁₁,d₂₂,…,d_rr; в противном случае эти преобразования позволяют получить из системы уравнение вида (2), где b – число, отличное от нуля.

Задача 1. Решить систему уравнений:

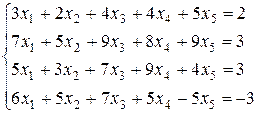
Решение. Если условиться писать неизвестные только в порядке воз­растания номеров, то сами символы неизвестных становятся лишними, важны лишь коэффициенты. Поэтому систему линейных уравнений удобно записы­вать и решать в виде расширенной матрицы, т.е. в виде прямоуголь­ной таб­лицы коэффициентов (вертикальной чертой отделены свободные члены).

Выписываем расширенную матрицу системы и проводим прямой ход схемы Гаусса (пояснения приведены ниже):

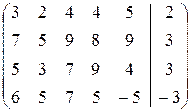
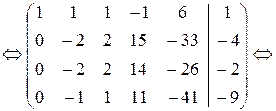
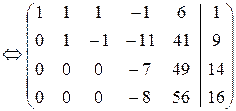
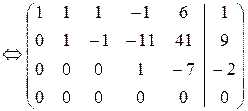
Чтобы получить единицу в верхнем левом углу матрицы, первую строку умножаем на 2 и вычитаем из нее третью. Полученную новую строку, умноженную на (–7), (–5) и (–6) соответственно, прибавляем ко вто­рой, третьей и четвертой строкам. Результатам этих операций является вторая из написанных матриц. Далее, четвертую строку умножаем на (–1) и пере­ставляем ее со второй, и прибавляем эту новую вторую строку, умноженную на 2, к третьей и четвертой строкам; результат – третья матрица. Теперь тре­тью строку умножаем на (–1/7), полученную новую третью строку, умножен­ную на 8, прибавляем к четвертой. Прямой ход закончен.

Выписываем систему, соответствующую последней матрице:

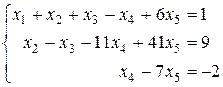
Проведем обратный ход. Здесь главные неизвестные x₁,x₂,x₄;
свободные – х₃, х₅, придаем им произвольные значения: х₃=a, x₅=b. Двигаясь по послед­ней системе снизу вверх, выражаем главные неизвестные через свободные.

Запись обратного хода целесообразно вести так.
Запишем заготовку ответа:

x₁=

x₂=

x₃=

x₄ =
затем будем вписывать в нее произвольные значения неизвестных

x₁=

x₂=a

x₃=

x₄=b
и далее последовательно получаем значения остальных неизвестных:

x₁ =1–(–13+ a +36 b)– a +(–2+7 b)–6 b =12–2 a –35 b,

x₂ =9+ a +11(–2+7 b)–41 b =–13+ a +36 b,

x₃ = a,

x₄ =–2+7 b,

x ₅= b,
где a, b – любые числа.

Ответ: (12–2 a –35 b, –13+ a +36 b, a, –2+7 b, b)

Задача 2. Решить систему уравнений

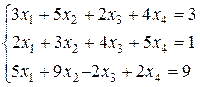
Решение. В расширенной матрице сначала вычитаем вторую строку из первой, чтобы получить единицу в верхнем левом углу матрицы, а затем но­вой первой строкой получаем нули в 1-м столбце; далее, из новой третьей строки вычитаем новую вторую:

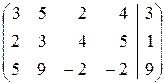
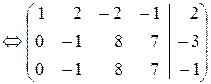
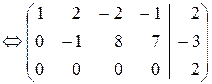
Последняя строка последней матрицы даёт уравнение 0=2, не имеющее решений. Значит, система несовместна.

Ответ: система несовместна.

Задача 3. Решить систему уравнений

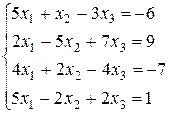
Решение. В расширенной матрице из первой строки вычитаем третью и получаем этой строкой нули в первом столбце, далее, второй строкой по­лучаем нули во втором столбце и т.д.:

, .
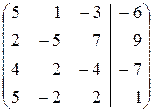
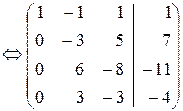
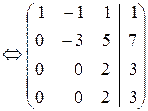
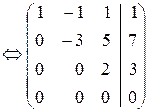
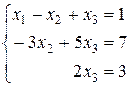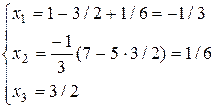Cвободных неизвестных нет, поэтому решение единственно.

Ответ: (–1/3, 1/6, 3/2).

Задача 4. Решить следующую систему уравнений в зависимости от параметра:

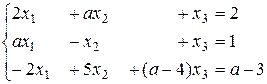
Решение. Выпишем расширенную матрицу системы и приведем её к ступенчатому виду.

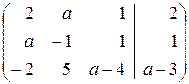
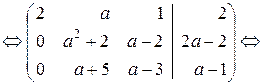
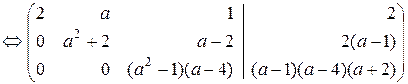
При а =–1 последняя строка матрицы соответствует уравнению 0=1, которое не имеет решений. Следовательно, при а =–1 система не имеет реше­ний.

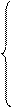При а =1 матрица имеет вид:
,

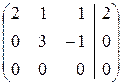
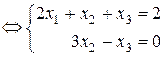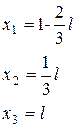
При а=4 матрица имеет вид:
, ,

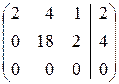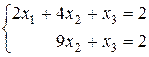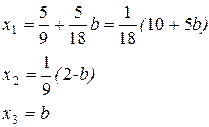
При 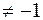а 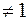, а , а 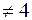матрица имеет вид:
,

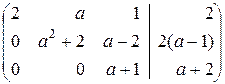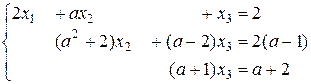
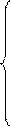
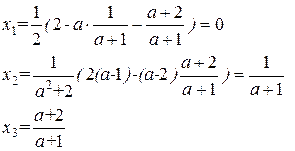
Ответ:

· если а =–1, то система несовместна;

· если а =1, то система совместна неопределенная с реше­нием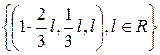

· если а =4, то система совместно неопределенная с
решением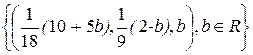

· если а 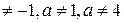то система совместно определенная с решением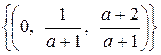

Для самостоятельного решения.

1. Решить системы уравнений:
а) 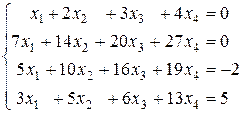б)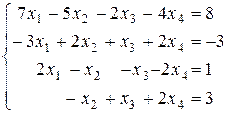
в)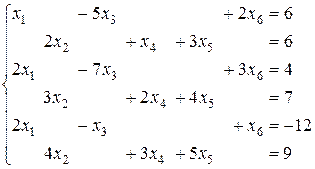

2. Решить при различных значениях параметра системы уравнений:

а) 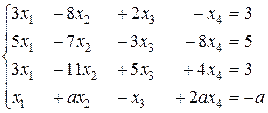б) .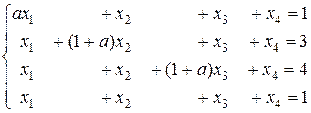

§2. Арифметическое n-мерное векторное пространство. Линейная зави­симость и независимость. Базис и ранг системы векторов.

Определение арифметического вектора. Сложение векторов, умно­же­ние вектора на число. Свойства этих операций. Линейная комбинация векто­ров. Линейно зависимая и линейно независимы. Критерий линейной зависимо­сти системы векторов. Базис и ранг системы векторов. Эквивалент­ные сис­темы векторов и их свойства. Элементарные преобразования системы векто­ров.

Пусть Р ={a,b,c,d…} – числовое поле, Pⁿ={a,b,g,…} – множество векторов. Арифметическим n–мерным вектором называется любой упорядоченный набор n чисел поля P, т.е. a=(a₁,a₂,…,a_n), где a_iÎP (i=1..n). Числа a₁,a₂,…,a_n, записанные в указанном порядке, называются координатами вектора.

Если a=(a₁,a₂,…,a_n), b=(b₁,b₂,…,b_n) ÎPⁿ, тогда определяют:

1. a=bÛ a₁=b₁, a₂=b₂,..., a_n=b_n;

2. a+b=(a₁+b₁,a₂+b₂,...,a_n+b_n)

3. k a=(k a₁, k a₂,…, k a_n), где k ÎP.

Вектор q=(0,0,...,0)Î Pⁿ называется нулевым вектором. Вектор
–a=(–1)a=(–a₁,–a₂,…,–a_n) называется противоположным вектору a.

Операция сложения векторов из Pⁿ обладает следующими свойствами:

1. "a, b ÎPⁿ a+b=b+a (коммутативность);

2. "a, b,g ÎPⁿ (a+b)+g=a+b+g (ассоциативность);

3. "aÎPⁿ a+q=a (q–нейтральный элемент относительно операции сложения векторов);

4. "aÎPⁿ $(–a)ÎPⁿ a+(–a)=q,где (–a) является элементом симметричным элементу a относительно операции сложения.

Операция умножения вектора на скаляр обладает следующими свойст­вами:

5. "aÎPⁿ 1a=a, где 1–единица поля P;

6. "aÎPⁿ "a, bÎ P a(ba)=(ab)a.

Операция умножения вектора на скаляр связана с операциями сложения двумя дистрибутивными законами:

7. "aÎ Pⁿ "a, bÎ P (a+b)a =aa+ba;

8. "aÎ P "a,bÎ Pⁿ a(a+b)=aa+ab.

Перечисленные свойства доказываются непосредственной проверкой.

Множество Pⁿ всех n-мерных арифметических векторов, в котором опреде­лены опе­рации сложения векторов и умножения вектора на элементы из поля P (указанным выше способом), называется n-мерным арифметическим вектор­ным пространством над полем P.

Например, Rⁿ – n-мерное арифметическое пространство, вектора кото­рого имеют действительные координаты.

Условимся под системой векторов арифметического пространства Pⁿ по­нимать конечный упорядоченный набор векторов этого пространства.

Пусть a₁,a₂,…,a_m – некоторая система векторов пространства Pⁿ. Век­тор a=a₁a₁+a₂a₂+…+a_ma_m называется линейной комбинацией векторов ука­занной системы, числа a₁,a₂,…,a_m – коэффициенты этой линейной комбина­ции. Гово­рят также, что вектор a линейно выражается через вектора a₁,a₂,…,a_m.

Если вектор a линейно выражается через вектора системы a₁,a₂,…,a_m, а каждый из векторов a_I линейно выражается через вектора системы b₁,b₂,…,b_k, то вектор a линейно выражается через вектора b₁,b₂,…,b_k.

Линейная комбинация системы векторов называется нетривиальной, если хотя бы один её коэффициент отличен от нуля, и тривиальной, если все её коэф­фициенты равны нулю.

Cистема векторов называется линейно зависимой, если существует ее нетривиальная комбинация, равная нуле­вому вектору.

Система векторов называется линейно независимой, если всякая ее линейная комбинация, равная нулевому вектору, тривиальная.

Система, состоящая из одного нулевого вектора, линейно зависима.

Теорема 1. (критерий линейной зависимости системы векторов). Сис­тема векторов линейно зависима тогда и только тогда, когда хотя бы один из ее векторов линейно выражается через остальные или она состоит только из нулевого вектора.

Вопрос о линейной зависимости можно свести к вопросу о наличии ненулевых решений у соответствующей системы линейных однородных уравнений. Рассмотрим, например, систему векторов:

a₁=(1,1,2); a₂=(–2,1,–1); a₃=(–1,2,1)

Выясним, при каких значениях коэффициентов ее линейная комбина­ция равна нулевому вектору. Пусть x ₁a₁+ x ₂a₂+ x ₃a₃=q

Распишем это векторное равенство:
x₁a₁ =(x₁,x₁,2x₁)
+ x₂a₂ =(–2x₂,x₂,–x₂)
x₃a₃ =(–x₃,2x₃,x₃)
–––––––––––––––––
(0,0,0)=q=(x₁–2x₂–x₃,x₁+x₂+2x₃,2x₁–x₂+x₃),
откуда по определению равенства арифметических векторов .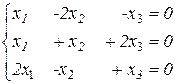

Решаем полученную систему линейных уравнений методом Гаусса:

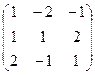
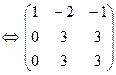
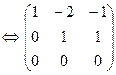
Cистема уравнений является неопределенной и имеет ненулевые реше­ния. Следовательно, данная система векторов линейно зависима. Общее ре­шение системы имеет вид {(–а,–a,a)| a ÎR}, и при а =–1 получаем частное решение (1,1,–1). Тогда 1×a₁+1×a₂–1a₃=q.

Аналогичными рассуждениями доказывается линейная независимость системы единичных векторов:
e₁=(1,0,0,…,0),
e₂=(0,1,0,…,0),
…………………
e_n=(0,0,0,…,1),
а также линейная независимость ступенчатой системы векторов, примером кото­рой может служить система
a₁=(a₁₁,a₁₂,…,a_1r,…,a_1n),
a₂=(0,a₂₂,…,a_2r,…,a_2n),
a_r=(0, 0,…,a_rr,…,a_rn),
где а₁₁, а₂₂, …,a_rr¹0

Теорема 2. (основная теорема о линейной зависимости). Если сис­тема векторов a₁,…,a_k линейно выражается через систему b₁,…,b_s и k>s, то пер­вая система линейно зависима. Следовательно, всякая система из k
n-мерных векторов при k>n линейно зависима.

Базисом системы векторов называется такая ее линейно незави­симая (упорядоченная) подсистема, через которую линейно выражаются все вектора системы.

Система, состоящая только из нулевых векторов, базисом не обла­дает, так как в этом случае невозможно выделить ее линейно независимую под­систему. Линейно независимая система векторов сама является собст­венным базисом. У линейно зависимой системы может быть более одного базиса.

Две системы векторов называются эквивалентными, если каждая из них линейно выражается через другую.

Всякая система векторов эквивалентна своему базису, так как каж­дый вектор a системы выражается, притом единственным образом, через базисные векторы a₁,…,a_k этой системы в виде линейной комбинации a=а₁a₁+…+a_ka_k. Набор (а₁, а₂, …,a_k) называют координатами вектора a в базисе (a₁, a₂,…,a_k). Любые два базиса одной и той же системы векто­ров также эквива­лентны. К эквивалентным системам приводят их элемен­тарные преобразо­вания, к которым относятся:

1) умножение любого вектора системы на отличное от нуля число;

2) прибавление к одному из векторов системы другого вектора системы ум­ноженного на число;

3) исключение из системы (включение в систему) вектора, являющегося ли­нейной комбинацией остальных;

4) перестановка любых двух векторов системы.

Эквивалентность всех базисов одной системы векторов и основная тео­рема о линейной зависимости позволяют утверждать, что любые два базиса одной и той же системы векторов содержат одинаковое количество векторов.

Рангом системы векторов называется число векторов в ее базисе. Или иначе, ранг системы векторов — это максимальное число ее линейно независимых векторов.

У эквивалентных систем векторов эквивалентны базисы, поэтому эк­вивалентные системы векторов имеют одинаковые ранги. Следовательно, элементарные преобразования системы векторов не изменяют ее ранга.

Все изложенное относится и к арифметическим векторам над нечи­словыми полями, с той лишь разницей, что везде вместо число следует го­ворить “ элемент поля Р ”.

Задача 1. Найти линейную комбинацию b=2a₁–4a₂+5a₃ системы век­торов a₁=(2,1,2,1); a₂=(–3,1,5,4); a₃=(3,2,0,1).

Решение. Используя определения произведения числа на вектор и суммы векторов, получаем

2a₁= (4,2,4,2)

+ –4a₂= (12,–4,–20,–16)

5a₃= (15,10,0,5)

b= (31,8,–16,–9)

Ответ: b= (31,8,–16,–9).

Задача 2. Выяснить, зависима или независима система векторов, найти один из ее базисов и вычислить ранг, выразить небазисные векторы через выбранный базис:
a₁=(2,1,–1,3); a₂=(–1,3,–2,1); a₃=(1,2,3,–1); a₄=(1,12,5,–1); a₅=(5,0,13,–5);

Решение. I cпособ. Следует выяснить при каких значениях х₁,x₂,x₃,x₄,x₅, имеет место равенство:

x₁a₁+x₂a₂+x₃a₃+x₄a₄+x₅a₅=0 (1)

Запишем векторное равенство (1) в виде системы однородных линей­ных уравнений:

2x₁ –x₂ +x₃ +x₄+ 5x₅ = 0
x₁+3x₂+2x₃+12x₄ =0 (2)
– x₁ –2x₂+3x₃ +5x₄+13x₅=0
3x₁+x₂ –x₃ –x₄ –5x₅=0

Решаем систему (2) методом Гаусса:
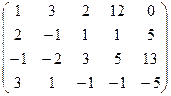
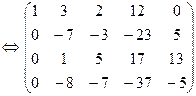
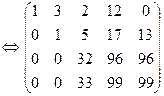Û
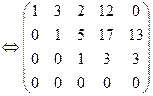
x₁+3x₂+2x₃+12x₄ =0
x₂+5x₃+17x₄ +13x₅=0
x₃+3x₄+ 3x₅ =0
где х₁,x₂,x₃ – главные неизвестные; х ₄, х ₅ –свободные неизвестные.
x ₁=–3(–2а+2b)–2(–3а–3b)–12а=0,
x ₂=–5(–3а–3b)–17а–13b=–2а+2b,
x ₃=–3а–3b,
x ₄= а,
x ₅= b.

Общее решение системы (2): {(0,–2а+2b,–3a–3b,a,b)ça,bÎR}. Таким об­разом, система (2) имеет ненулевые решения, следовательно, система векто­ров a₁,a₂,a₃,a₄,a₅ – линейно зависимая.

Векторы a₁,a₂,a₃, соответствующие по номерам главным неизвестным x₁,x₂,x₃, образуют базис. Докажем это. Подставим в (1) найденное решение:
0a₁+(–2а+2b) a₂+(–3a–3b) a₃+aa₄+ba₅=q (3)

Покажем, что система a₁,a₂,a₃ линейно независима. Для этого рассмот­рим равенство

y₁a₁+y₂a₂+y₃a₃=q (4)
или
y₁a₁+y₂a₂+y₃a₃+0a₄+0a₅=q (5)
Так как (5) содержится в (3), то

y ₁=0

y ₂=–2а+2b y ₁=0

y ₃= –3a–3b или y ₂=0 (6)

0=a y ₃=0

0=b

Итак, равенство (4) выполняется только при условии (6). Следова­тельно, система a₁,a₂,a₃, линейно независима.

Покажем, что все векторы системы a₁,a₂,a₃,a₄,a₅ выражаются через векторы a₁,a₂,a_3. Пологая в (3) а =1, b=0, получим a₄=0a₁+2a₂+3a₃; при а=0, b=1, получим a₅=0a₁– 2a₂ +3a₃.

II cпособ. Элементарными преобразованиями систему a₁,a₂,a_.3 ,a₄,a₅ приведем к лестничному виду. Для этого выпишем матрицу координат век­торов-строк и проведем элементарные преобразования системы ее строк:
~

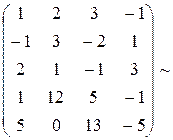
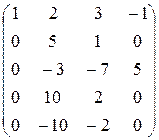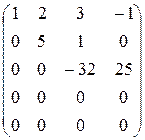
Преобразования осуществлялись только с помощью первых трех строк, а четвертая и пятая строки аннулировались, следовательно, можно ут­верждать, что a₄ и a₅ линейно выражаются через a₁,a_2,a₃. Кроме того, сис­тема век­торов a₁,a₂,a₃ линейно независима, так как эквивалентная ей сис­тема из первых трех строк последней матрицы линейно независима, ибо имеет лестничный вид. Итак, a₁,a₂,a₃ образует базис системы a₁,a₂,a₃,a₄,a₅, ранг которой равен 3.

Для вычисления коэффициентов линейных комбинаций a₄= x₁ a₁+ x ₂a₂+ x ₃a₃; a₅= y ₁a₁+ y ₂a₂+ y ₃a₃, запишем их в виде систем линейных уравнений:

2 x ₁ – x ₂ + x ₃=1 2 y ₁– y ₂+ y ₃ =5
x ₁+ 3x₂ + 2x₃ =12, y ₁+3 y ₂+2 y ₃=0
– x ₁ –2 x ₂+3 x ₃=5 – y ₁–2 y ₂+3 y ₃=13
3 x ₁ +x₂ – x ₃=–1 3 y ₁+ y ₂ – y ₃=–5.

Эти системы отличаются только обозначениями неизвестных и столб­цами свободных членов, поэтому их можно решать одновременно, записав рядом два столбца свободных членов (пакет двух систем линей­ных уравне­ний):
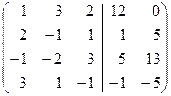
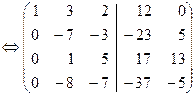
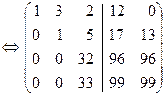Û

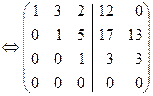
x ₁+3 x ₂+2 x ₃=12 x ₁=0
x ₂+5 x ₃=17, x ₂=2
x ₃=3 x ₃=3.

y ₁+3 y ₂+2 y ₃=0 y ₁=0
y ₂ +5 y ₃=13, y ₂=–2
y ₃=3 y ₃=3.

a₄=0a₁+2a₂+3a₃, a₅=0a₁–2a₂+3a₃.

Ответ: система векторов линейно зависима, один из ее базисов a₁,a₂,a₃, ранг системы равен 3, a₄₌0a₁+ 2a₂+3a₃, a₅=0a₁–2a₂+3a₃.

Задача 3. Пользуясь элементарными преобразованиями установить ли­нейную зависимость или независимость системы векторов:
a₁= (1,–2,2); a₂=(2,0,1); a₃=(–1,–3,4).

Решение. Элементарные преобразования приводят к системе экви­ва­лентной данной. Преобразуем по методу Гаусса матрицу координат-сток данных векторов
~ ~ ~

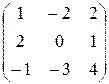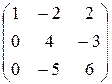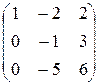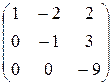
Система b₁=(1,–2,2), b₂=(0,–1,3), b₃=(0,0,–9) эквивалентна данной сис­теме и линейно независима (как лестничная система). Ранг полученный системы равен 3. Следовательно, система a₁,a₂,a₃ – линейно независима.

Ответ. Система векторов a₁,a₂,a₃ –линейно независима.