2015-07-04
921
Пусть на плоскости в дана аффинная система координат R=(О,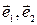 
) и дана прямая ℓ, пересекающая ось ординат.
Если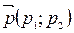 
− направляющий вектор прямой, то 
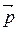и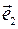 
не коллинеарны, поэтому 
.
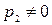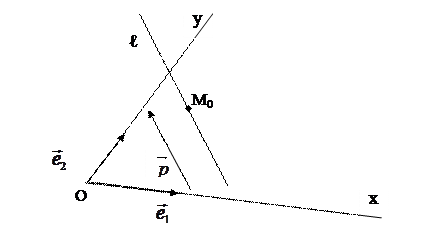
Рис.9
Число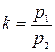 
называется угловым коэффициентом прямой ℓ. Заметим, что угловой коэффициент прямой не зависит от выбора направляющего вектора прямой. Действительно, если 
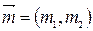− другой направляющий вектор прямой ℓ, то 
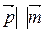поэтому координаты векторов 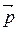и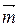 
пропорциональны 
.
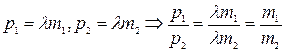Пусть k − коэффициент прямой ℓ, координат R=(О, 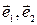). Очевидно, что если 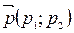направляющий вектор прямой ℓ, то вектор 
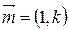является направляющим вектором этой прямой. Поэтому уравнение (5) можно записать в виде 
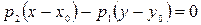или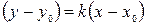 
.
|
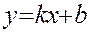
Если в качестве точки М(х0;у0) взять точку В(0;b), то последнее уравнение примет вид
(8)
Это уравнение называется уравнением прямой с угловым коэффициентом.
Угловой коэффициент k прямой имеет простой геометрический смысл, если прямая задана в прямоугольной системе координат R(O,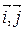 
).
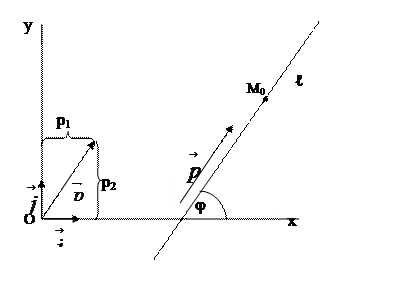
Рис.10
Всамом деле, если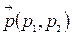 
направляющий вектор прямой ℓ, то 
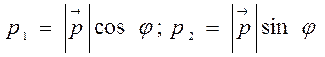, где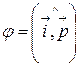 
. Таким образом, 
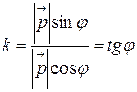. Последнее соотношение показывает, что в прямоугольной системе координат угловой коэффициент прямой равен тангенсу угла наклона прямой к оси Ох.
|
|
|
