А ) Уравнение прямой, заданной точкой и направляющим вектором

Поставим перед собой задачу получить уравнение прямой . Введём на плоскости аффинную систему координат R=(О, 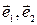) и рассмотрим прямую ℓ, заданную точкой М_о(х_о,у_о) и вектором 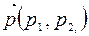параллельным ей.

Рис.8

В этом случае положение прямой ℓ на плоскости определяется единственным образом.

Пусть точка М(x;y) − произвольная точка прямой ℓ. Очевидно, что точка М(x,y) 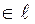тогда и только тогда, когда векторы 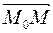и 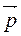параллельны. => 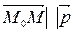. Координаты вектора 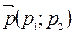и вектора

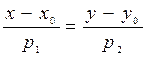
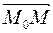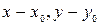() известны, =>

(5)

Уравнение (5) называется уравнением прямой заданной точкой и направляющим вектором или каноническим уравнением прямой.

б) Параметрические уравнения прямой.

Заметим, что уравнения (5)можно записать в виде:

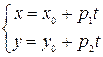
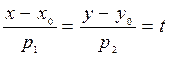или (6).

Уравнения (6) называются параметрическими уравнениями прямой.