В ) Уравнение прямой, проходящей через две точки

Согласно аксиомам планиметрии через две точки плоскости проходит единственная прямая.

Пусть на плоскости введена аффинная система R=(О, 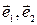) координат и даны две точки, которые имеют координаты М₁(х₁;у₁) и М₂ (х₂;у₂). (Рис. 8.)

В этом случае в качестве направляющего вектора прямой можно взять вектор .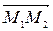

Рис.8

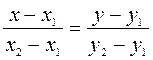
Таким образом направляющий вектор прямой ℓ 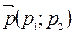= = =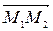(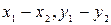). Уравнение прямой (М₁М₂) в этом случае запишется в виде:

(7)

Уравнение (7) называется уравнением прямой проходящей через две точки.