Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
Расстояние от точки М до плоскости α вычисляется по формуле 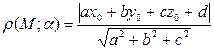 , где М(х0;у0;z0), плоскость α задана уравнением ax+by+cz+d=0.
, где М(х0;у0;z0), плоскость α задана уравнением ax+by+cz+d=0.
Пример 1.В правильной четырехугольной пирамиде со стороной основания, равной 2 и высотой, равной 4, найти расстояние от точки А до плоскости (SBC).
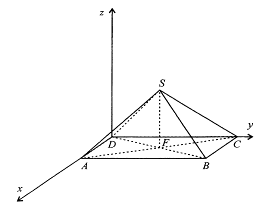
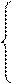 Решение: Введем прямоугольную систему координат с началом в точке D(0;0;0). Составим уравнение плоскости (SBC), используя координаты точек В(2;2;0), С(0;2;0), S(1;1;4) и решив систему уравнений:
Решение: Введем прямоугольную систему координат с началом в точке D(0;0;0). Составим уравнение плоскости (SBC), используя координаты точек В(2;2;0), С(0;2;0), S(1;1;4) и решив систему уравнений:
a∙ 2+ b ∙2+c∙0+d = 0
a ∙ 0 +b ∙ 2 +c∙0+d = 0
a ∙1 +b ∙1 +c∙4+d = 0.
Получим, что d= -2∙ b, a=0, c = 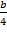 . Таким образом, уравнение плоскости примет вид:
. Таким образом, уравнение плоскости примет вид:
0∙х +4∙у + z - 8 =0. Значит, a=0, b=4, c=1, d=- 8.
Точка А, расстояние от которой до плоскости нужно найти, имеет координаты:
А(2;0;0). Значит, 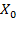 =2,
=2, 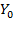 = 0,
= 0, 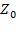 =0. По формуле нахождения расстояния от точки до плоскости имеем:
=0. По формуле нахождения расстояния от точки до плоскости имеем:
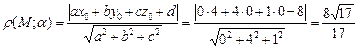
Ответ: 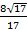 .
.
 2015-07-04
2015-07-04 696
696







