Нахождение угла между прямой и плоскостью

• Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и её проекцией на данную плоскость.
• 0 ˚<(a,α)<90˚.

Угол между прямой l и плоскостью α можно вычислить по формуле 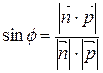или в координатах 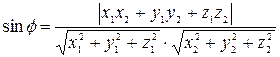, где 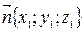- вектор нормали к плоскости α, 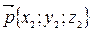- направляющий векор прямой l;

Пример 1. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ рёбра АВ и АА₁ равны 1, а ребро АD=2. Точка Е – середина ребра В₁С₁. Найдите угол между прямой ВЕ и плоскостью (АВ₁С).

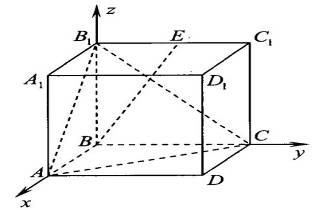
Решение: Составим уравнение плоскости (АВ₁С.):

ах+bу+cz+d=0, где a, b и c – координаты нормали к плоскости.

Чтобы составить это уравнение, необходимо определить координаты трёх точек, лежащих в данной плоскости: А(1; 0; 0), В₁(0;0;1), С(0;2;0).

Решая систему

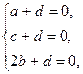
находим коэффициенты а, b и с уравнения ах+bу+cz+d=0: а= -d, b= 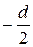, c=-d. Таким образом, уравнение примет вид 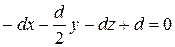или, после упрощения, 2х+у+2z-2=0. Значит, нормаль n к этой плоскости имеет координаты .

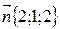Найдем координаты вектора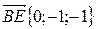

Найдем угол между вектором 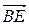и нормалью к плоскости по формуле скалярного произведения векторов:

.

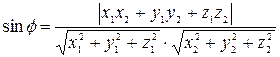
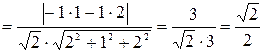Ответ: 45˚