Составление уравнений состояния цепей на основании законов Кирхгофа

Из предыдущих разделов известно, что в общем случае, когда цепь содержит n_В ветвей (в том числе n_T источников тока) и n_у узлов, число неизвестных токов (напряжений) равно n_В - n_у + 1 - n_T. Для отыскания такого числа неизвестных составляется система уравнений по законам Кирхгофа.

По первому закону Кирхгофа (ЗТК) записывается nу - 1 уравнений вида:

,

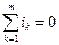где m - число ветвей, сходящихся в узле.

По второму закону Кирхгофа (ЗНК) записывается n_В - n_у + 1 уравнений вида:

,

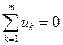где n - число ветвей, входящих в контур.

Если цепь содержит, кроме линейных, также и НЭ, то в системе уравнений, описывающей состояние цепи, появятся уравнения вида i_K=F_k(u_k). Методика составления уравнений состояния цепи на основе законов Кирхгофа остается такой же, как и в случае линейных резистивных цепей.

Составим, например, систему уравнений состояния для цепи, схема которой изображена на рис. 25 Пусть ВАХ нелинейного элемента аппроксимируется выражением

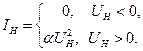(14)

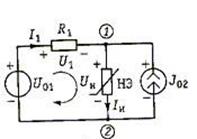
Рис. 25. Схема цепи

Зададимся положительными направлениями напряжений и токов. Цепь содержит один независимый контур (I) и один независимый узел (1). Уравнения, записанные по ЗТК и ЗНК, имеют следующий вид:

I₁ + J₀₂ - I_H = 0; (15)

I₁R₁ + U_H - U₀₁ = 0 (16)

К этим уравнениям дописываем уравнение (14). Неизвестными в данной системе уравнений являются напряжение (U_H и токи I₁ и I_H). Всего три неизвестных. Для их отыскания составлено три уравнения. Как видим, процесс составления системы уравнений такой же, как и в случае линейной цепи. Однако процесс решения полученной системы, которая содержит нелинейное уравнение, может существенно затрудниться. Для большинства относительно сложных цепей аналитического решения системы уравнений может и не существовать. Тогда приходится прибегать к численным методам решения.

В рассматриваемом примере достаточно просто получить аналитическое решение. Предположим вначале, что решение системы уравнений существует при U_H > 0. Тогда уравнение НЭ имеет вид

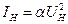. (17)

Выразим из уравнения (15) ток I₁ = I_H - J₀₂ и подставим его в уравнение (16). В результате этой операции получим

I_HR₁ - J₀₂R₁+ U_H - U₀₁= 0 (18)

Подставив в (18) выражение (17), получим уравнение относительно неизвестного напряжения на нелинейном двухполюснике

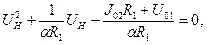(19)

Отсюда имеем

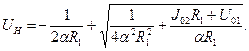(20)

Пусть R₁ = 1 кОм, U₀₁ = 14 В J₀₂ =10 мА, α = 10-5 А/В. Тогда U_H =20 В. Второе решение уравнения (19) даст U_H < 0. Это решение не подходит, так как применялось уравнение НЭ, справедливое при U_H > 0.

Допустим теперь существование решения системы уравнений (15) - (16) при U_H < 0. Согласно уравнению НЭ (14) I_H = 0, Тогда из уравнения (18) имеем

U_H = J₀₂R₁ + U₀ = 24 В > 0,

а это противоречит условию, что U_H < 0.

Таким образом, остается первое решение (20). Найдем остальные неизвестные. Из (17) имеем I_H= αU²_H = 10^-5 ∙10² = 4мА, а из (15) I_H -J₀₂ = -6 мА.

В данном примере получено аналитическое решение системы нелинейных уравнений. Если бы ВАХ нелинейного элемента описывалась более сложной функцией, то этого достичь не удалось бы.