Часто необходимо иметь аналитические выражения для вольт-амперных характеристик нелинейных элементов. Эти выражения могут лишь приближенно представлять ВАХ, поскольку физические закономерности, которым подчиняются зависимости между напряжениями и токами в электронных и полупроводниковых приборах, не выражаются аналитически.
Задача приближенного аналитического представления функции, заданной графически или таблицей значений, в заданных пределах изменения ее аргумента (независимой переменной) предполагает, во-первых, выбор аппроксимирующей функции, т. е. функции, с помощью которой приближенно представляется заданная зависимость, и, во-вторых, выбор критерия оценки “близости” этой зависимости и аппроксимирующей ее функция.
В качестве аппроксимирующих функций используются, чаще всего, алгебраические полиномы, некоторые дробные рациональные и трансцендентные функции или совокупность отрезков прямых линий.
Будем считать, что ВАХ нелинейного элемента i = F(u) задана графически, т. е. определена в каждой точке интервала Umin ≤ u ≤ Umаx, и представляет собой однозначную непрерывную функцию переменной u. Тогда задача аналитического представления вольт-амперной характеристики может рассматриваться как задача аппроксимации заданной функции ξ(х) выбранной аппроксимирующей функцией f(x).
О близости аппроксимирующей f(x) и аппроксимируемой ξ(х) функций или, иными словами, о погрешности аппроксимации, обычно судят по наибольшему абсолютному значению разности между этими функциями в интервале аппроксимации а ≤ х ≤b, т. е. по величине
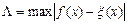 . (10)
. (10)
Часто критерием близости выбирается среднее квадратическое значение разности между указанными функциями в интервале аппроксимации, т. е, величина
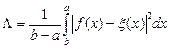 .
.
Иногда под близостью двух функций f(x) и ξ(х) понимают совпадение в заданной точке х =Х0 самих функций и п + 1 их производных.
Наиболее распространенным способом приближения аналитической функции к заданной является интерполяция (метод выбранных точек), когда добиваются совпадения функций f(x) и ξ(х) в выбранных точках (узлах интерполяции) xk, k = 0, 1, 2,..., n.
Погрешность аппроксимации может быть достигнута тем меньшей, чем больше число варьируемых параметров входит в аппроксимирующую функцию, т. е., например, чем выше степень аппроксимирующего полинома или чем больше число отрезков прямых содержит аппроксимирующая линейно-ломаная функция. Одновременно с этим, естественно, растет объем вычислении как при решении задачи аппроксимации, так и при последующем анализе нелинейной цепи. Простота этого анализа наряду с особенностями аппроксимируемой функции в пределах интервала аппроксимации служит одним из важнейших критериев при выборе типа аппроксимирующей функции.
В задачах аппроксимации вольт-амперных характеристик электронных и полупроводниковых приборов стремиться к высокой точности их воспроизведения, как правило, нет необходимости ввиду значительного разброса характеристик приборов от образца к образцу и существенного влияния на них дестабилизирующих факторов, например, температуры в полупроводниковых приборах. В большинстве случаев достаточно “правильно” воспроизвести общий усредненный характер зависимости i = F(u) в пределах ее рабочего интервала.
Полиномиальная аппроксимация. В качестве аппроксимирующей функции в задачах аналитического представления вольт-амперных характеристик очень часто используются алгебраические полиномы
f(x) = a0 + a1x + a2x2 +...anxn
той или иной степени.
Постоянные a0, a1, a2,..., an представляют собой варьируемые параметры, значения которых выбираются такими, чтобы в интервале аппроксимации а ≤ х ≤b свести к минимуму погрешность аппроксимации в соответствии с выбранным критерием близости.
В простейшем случае критерием близости может служить совпадение значений аппроксимирующей и аппроксимируемой функций в возможно большем числе выбранных точек, расположенных в интервале аппроксимации. Соответствующий метод приближенного воспроизведения функций носит, как мы уже упоминали, название интерполирования, а дискретные точки, в которых требуется точное совпадение функций f(x) и ξ(х), называются узлами интерполирования. Их число на единицу превышает степень интерполирующего полинома. Действительно, записывая равенство функций f(xk) = ξ(хk) в каждом из узлов интерполирования xk, k = 0, 1, 2,..., n, получим систему из n + 1 линейных уравнений
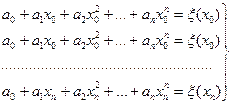 (11)
(11)
с таким же числом неизвестных коэффициентов a0, a1, a2,.., an интерполирующего полинома.
В теории интерполирования функций доказывается, что система уравнений (11) имеет единственное решение. Единственным, следовательно, будет и решение рассматриваемой задачи интерполирования вольт-амперной характеристики полиномом выбранной степени.
Приведем простейший пример интерполирования в интервале 0≤ х ≤1,5 полиномом первой степени f(x) =a0+ a1х функции ξ(х) =1- е-х, заданной аналитически. Расположим узлы интерполирования, а их должно быть п + 1 = 2, при x 0 = 0,1 и х 1 = 1,0. Тогда система уравнений относительно искомых коэффициентов а0 и а1 будет такой: а0 + а1 ∙ 0,1 = =1- е-0,1 и а0 + а1 = 1- е-1. Из ее решения следует а0 = 0,036, а1 = 0,597 и f(x) = 0,036 + 0,597x. Графики функций f(x) и ξ(х) приведены на рис. 17. Они показывают, что точность воспроизведения заданной функции невелика. В заданном интервале 0≤ х ≤ 1,5 наибольшая погрешность | f(x) - ξ(x) |, т. е. max| f(x) - ξ (x) | находится на одной из границ интервала при х =-1,5 и составляет 0,158. Ее можно уменьшить, выбрав другие узлы интерполирования и, тем более, повысив степень интерполирующего полинома. Так, графики той же функции ξ (х) =1- е-х и интерполирующего полинома второй степени с узлами интерполирования x 0= 0,15, х 1= 0,6 и х 2= 1,2 практически совпадают.
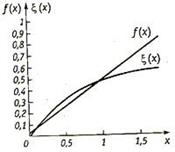
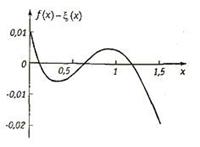
Рис. 17. Графики функций f(x) и ξ(х) Рис. 18. График разности функций
f(x) и ξ(х)
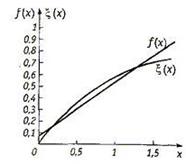
Рис. 19. Аппроксимирующей функция f(x) и функция ξ(х)
На рис. 18 приведен график разности этих функций, из которого следует, что погрешность в том же заданном интервале не превышает 0,026, т. е. уменьшилась по сравнению с линейной интерполяцией в 6 раз.
Одним из эффективных методов аппроксимации функций, в котором погрешность аппроксимации контролируется во всем интервале приближения а ≤ х ≤ b, а не в его дискретных точках, является метод наилучшего равномерного приближения (аппроксимации) функций (приближения по П. Л. Чебышеву). В этом методе параметры аппроксимирующей функции выбираются такими, чтобы в интервале приближения наибольшее по абсолютной величине отклонение функции f(x) от непрерывной функции ξ(х) было бы минимально возможным, или, используя обозначения (10), чтобы в интервале а ≤ х ≤ b
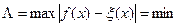 . (12)
. (12)
В рассмотренном выше примере этому критерию удовлетворяет полином f(x) = 0,071 + 0,518х. Наибольшие его отклонения от функции ξ(х) =1- е-х в интервале 0 ≤ х ≤1,5 расположены при х = 0, х = х m =0,658 и х =1,5 (см. рис. 19), причем, что очень важно, все они равны по абсолютной величине. Легко понять, что любое изменение наклона (a1) или уровня (a0) полинома f(x), которое ведет к уменьшению экстремального отклонения в двух из трех указанных точек, увеличивает отклонения в оставшейся точке. Таким образом, полином f(x) =0,071+0,518 х из всех полиномов первой степени действительно минимизирует абсолютную величину отклонения от функции 1- е-х в интервале 0 ≤ х ≤ 1.
В теории аппроксимации функций доказывается, что наибольшее по абсолютной величине отклонение полинома f(x) степени п от непрерывной функции ξ(х) будет минимально возможным, если в интервале приближения а ≤ х ≤ b разность f(x) - ξ(х) не меньше, чем п + 2 раза принимает свои последовательно чередующиеся предельные наибольшие f(x) - ξ(х) = L > 0 и наименьшие f(x) - ξ(х) = -L значения (критерий Чебышева).
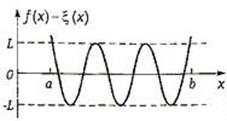
Рис. 20. Характер графика разности f(x) - ξ(х) для полинома f(x) пятой степени
Характер графика разности f(x) - ξ(х) для полинома f(x) пятой степени, удовлетворяющего этому критерию, приведен на рис. 20. Этому же критерию удовлетворяет полином f(x) в рассмотренном выше примере (см, рис. 18).
Во многих прикладных задачах находит применение полиномиальная аппроксимация по среднеквадратическому критерию близости, когда параметры аппроксимирующей функции f(x) выбираются из условия обращения в минимум в интервале аппроксимации а≤ х ≤b квадрата отклонения функции f(x) от заданной непрерывной функции ξ(х), т. е., из условия:
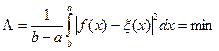 . (12.1)
. (12.1)
В соответствии с правилами отыскания экстремумов решение задачи сводится к решению системы линейных уравнении, которая образуется в результате приравнивания к нулю первых частных производных функции Λ по каждому из искомых коэффициентов ак аппроксимирующего полинома f(x), т. е. уравнений
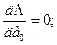
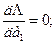
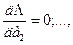
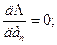
Доказано, что и эта система уравнений имеет единственное решение. В простейших случаях оно находится аналитически, а в общем случае - численно. Так, в рассматриваемом примере система уравнений при аппроксимации в интервале 0 ≤ х ≤ 1,5 функции 1- е-х полиномом первой степени такова:
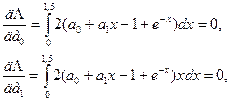
или после преобразований:
3 а0 + 2,25 а1 = 1 + 2 ∙ е-1,5; 2,25 а0 + 2,25 а1 = 0,25 - 5 ∙ е-1,5.
Заметим, что, как правило, средняя квадратическая погрешность наилучшего равномерного приближения функций f(x) и ξ(х) лишь не намного отличается от минимально возможной. Обратное утверждение обычно ошибочно, т. е. при квадратической аппроксимации в некоторых участках интервала аппроксимации возможны существенные превышения погрешности аппроксимации (выбросы) по сравнению с теми, которые соответствуют критерию (12).
Вернемся к вольт-амперным характеристикам. Общий вид записи степенного полинома, аппроксимирующего ВАХ:
I = а0 + а1u+ а2u2 +... + аnun
Иногда бывает удобно решать задачу аппроксимации заданной характеристики в окрестности рабочей точки U0. Тогда используют степенной полином другого вида:
I = а0 + а1(u - U0) + a2(u - U0)2 +... + an(u - U0)
Пример
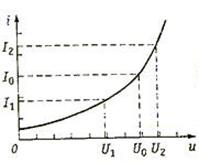
Рис. 21. ВАХ нелинейного резистпвного элемента
Используя метод интерполяции, аппроксимировать ВАХ нелинейного резистивного элемента (рис. 21) степенным полиномом. Аппроксимированная ВАХ должна совпадать с заданной в выбранных точках U0, U1 и U2.
Составим систему уравнений:
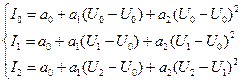
из которой найдём искомые коэффициенты
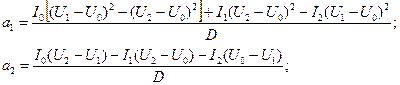
Пример
ВАХ нелинейного резистивного элемента i = F(u) задана таблицей:
| uк | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | |
| iк | 0.06 | 0.23 | 0.5 | 0.85 | 1.18 | 1.65 | 2.3 | 2.9 |
Используя квадратический критерий, аппроксимировать характеристику выражением i= а2u2.
Сумма квадратов отклонений аппроксимирующей функции от заданной:
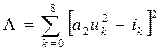
минимальна при значении коэффициента а2, удовлетворяющего уравнению
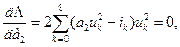 откуда
откуда 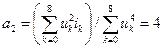
Пример
На рис. 22 кружочками показаны полученные экспериментально пять точек характеристики iБ = F(uБЭ) транзистора КТ301. Осуществим степенную аппроксимацию этой характеристики в диапазоне uБЭ от 0,4 до 0,9 В полиномом второй степени в окрестности рабочей точки U0 = 0,7 В.
Коэффициенты а0, a1,...,an полинома iБ = а0 + a1(uБЭ - U0)2 найдем, используя метод интерполяции. Выберем в качестве узлов интерполяции точки, соответствующие напряжениям 0,5; 0,7 и 0,9 В и составим систему уравнений:
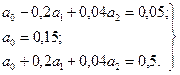
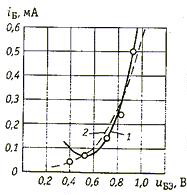
Рис. 22. Характеристики iБ = F(uБЭ) транзистора
Решение этой системы дает а0 = 0,15 мА, a1 = 1,125 мА/В, a2 =3,125 мА/В. Кривая тока iБ = 0,15 + 1,125(uБЭ - 0,7) + 3,125(uБЭ - 0,7)2 проходит через три экспериментальные точки, соответствующие узлам интерполяции (см. рис. 22, кривая 1). Из рисунка видно, что некоторые экспериментальные точки (например, при UБЭ = 0,4 В) плохо “ложатся” на эту кривую. Кроме того, появляется загиб в нижней части характеристики.
Лучшей аппроксимации можно добиться, если использовать полином четвертой степени п выбрать соответственно пять узлов интерполяции (0,4; 0,5; 0,7; 0,8; 0,9 В). В этом случае кривая тока iБ пройдет через все пять экспериментальных точек.
Однако можно попытаться сохранить вторую степень полинома и улучшить аппроксимацию, воспользовавшись каким-либо другим методом для определения коэффициентов аs. Найдем эти коэффициенты, используя среднеквадратическое приближение тока по всем пяти экспериментальным значениям.
Составим уравнения:
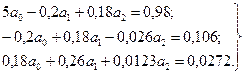
Решение этой системы уравнений дает: а0 = 0,164 мА, a1 = 1,07 мА/В и а2 = 2,069 мА/В2.
График тока при этом определяется полиномом
iБ = 0,164 + 1,07(uБЭ -0,7} + 2,069(uБЭ - 0,7)2
и показан на рис. 22, кривая 2. Эта характеристика является более приемлемой Для аналитического описания экспериментальных результатов.
 2015-07-04
2015-07-04 2035
2035








