Описание алгоритма венгерского метода

Венгерский алгоритм решения транспортной задачи линейного программирования (задачи о назначениях) состоит из предварительного этапа и не более чем n - 2 последовательно проводимых итераций. Каждая итерация связана с эквивалентными преобразованиями матрицы, полученной в результате проведения предыдущей итерации, и с выбором максимального числа независимых нулей. Окончательным результатом итерации является увеличение числа независимых нулей на единицу. Как только количество независимых нулей станет равным n, проблема выбора оказывается решенной. Оптимальный вариант назначений определяется позициями независимых нулей в последней матрице.

Основные понятия венгерского метода:

1. Две прямоугольные матрицы С = (c_ij) и С"= (с"_ij) размером m*n называются эквивалентными (С~С"), если с"_ij = с_ij + α_i +β_j;
i =1, 2,..., m; j = 1, 2,..., n. Задачи выбора, определяемые эквивалентными матрицами, являются эквивалентными, так как можно доказать, что множества оптимальных назначений двух задач выбора с эквивалентными матрицами совпадают.

2. Независимыми нулями называются нулевые элементы Z₁, Z₂,..., Z_k квадратной матрицы С, если для любого 1 ≤ i ≤ k строка и столбец, на пересечении которых лежит элемент Z_i, не содержит элементов Z_k для всех k≠i.

3. В процессе решения задачи некоторые строки (столбцы) матрицы С и эквивалентных ей матриц будут выделяться значком «+», стоящим справа от соответствующей строки (над соответствующим столбцом). Элементы, расположенные в выделенных строках или столбцах, будем называть выделенными элементами.

Предварительный этап. На этом этапе выполняются два последовательных преобразования матрицы С, в результате которых получается эквивалентная ей неотрицательная матрица С˝ в каждом столбце и каждой строке которой есть хотя бы один нуль.

Первое преобразование проделывается со всеми столбцами матрицы С. Из максимального элемента j-го столбца (i = 1, 2,..., n) вычитаются элементы этого столбца:

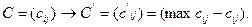
Полученная матрица С΄ является неотрицательной, и в каждом столбце этой матрицы имеется хотя бы один нуль.

Второе преобразование производится со строками матрицы С΄. Из элементов i-й строки матрицы С΄ вычитается минимальный элемент этой строки:

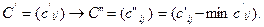
Если в каждой строке матрицы С' = (c΄_ij), полученной после первого преобразования матрицы С, уже имеется хотя бы один нуль, то второе преобразование не производится.

В результате предварительных преобразований осуществляется переход от задачи выбора на максимум с матрицей С к задаче выбора на минимум с матрицей С. Наименьшее возможное значение суммы n элементов неотрицательной матрицы равно, очевидно, нулю. Следовательно, задача сводится к выбору в матрице C˝ (или в эквивалентной ей матрице с неотрицательными элементами) n нулевых элементов, по одному в каждой строке и каждом столбце.

Отмечаем произвольный нуль в первом столбце звездочкой (*). Затем просматриваем второй столбец, и если в нем есть нуль, расположенный в строке, где нет 0*, то отмечаем его звездочкой. Аналогично просматриваются один за другим все остальные стол­бцы матрицы C˝. Очевидно, что нули матрицы C˝, отмеченные звездочкой, по построению являются независимыми.

(k + 1) итерация

Допустим, что k -я итерация проведена и в результате получена матрица С_к. Если в матрице С_к имеется ровно n нулей со звездочкой, то процесс решения заканчивается. Если же число нулей со звездочкой меньше n, то переходим к (k + 1) итерации. Каждая итерация начинается первым и заканчивается вторым этапом. Между ними может несколько раз проводиться пара этапов: третий—первый. Перед началом итерации знаком «+» выделяют столбцы матрицы С_k, которые содержат нули со звездочкой.

Первый этап. Просматривают невыделенные столбцы матри­цы С_k. Если среди них не окажется нулевых элементов, то переходят к третьему этапу. Если же невыделенный нуль матрицы С_k об­наружен, то возможен один из двух случаев: а) строка, содержа­щая невыделенный нуль, содержит также нуль со звездочкой; б) эта строка не содержит нуля со звездочкой.

В случае (а) невыделенный нуль отмечают штрихом и выделяют строку, в которой он содержится, знаком «+» справа от нее. Затем уничтожают знак «+», обводя его рамкой, над тем столбцом, на пересечении которого с данной выделенной строкой содержится нуль со звездочкой. Далее опять просматривают невыделенные стол­бцы, отыскивая в них невыделенные нули. Этот процесс за конеч­ное число шагов заканчивается одним из следующих исходов:

IA — имеется невыделенный нуль в строке, где нет нуля со звездочкой. В этом случае переходят ко второму этапу, отметив последний по порядку нуль штрихом.

IB — все нули матрицы С_k выделены, т. е. находятся в выделенных строках или столбцах. При этом переходят к третьему этапу.

В случае (б), отметив невыделенный нуль штрихом, сразу переходят ко второму этапу.

Второй этап. Строят следующую цепочку из нулевых элементов матрицы С_k. отмеченный последним нуль со штрихом, нуль со звездочкой, расположенный в одном столбце с ним, нуль со штри­хом, расположенный в одной строке с предшествующим нулем со звездочкой, и т. д. Итак, цепочка образуется передвижением от 0' к 0* по столбцу, от 0* к 0' по строке и т. д.

Можно доказать, что описанный алгоритм построения цепочки однозначен и конечен. При этом цепочка всегда начинается и закан­чивается нулем со штрихом (возможно, она будет состоять из од­ного нуля со штрихом). Далее, над элементами цепочки, стоящими на нечетных местах (0'), ставят звездочки, уничтожая их над четными элементами (0*). Затем уничтожают все штрихи над элементами матрицы С_k и знаки «+». При этом количество независимых нулей будет увеличено на единицу; (k+1) итерация закончена.

Третий этап. К этому этапу переходят после первого, если все нули матрицы С_k выделены, т. е. находятся в выделенных строках или столбцах. В таком случае среди невыделенных элементов матрицы С_k выбирают минимальный и обозначают его h > 0. Далее величину h вычитают из всех элементов матрицы С_k, расположенных в невыделенных строках, и прибавляют ко всем элементам, расположенным в выделенных столбцах. Получают новую матрицу С_k⁽¹⁾, эквивалентную С_k.

Поскольку среди невыделенных элементов матрицы С_k⁽¹⁾, появятся новые нули (согласно определению), переходят к первому этапу, при этом вместо матрицы С_k рассматривают матрицу С_k⁽¹⁾. Завершив первый этап, либо переходят ко второму этапу, либо вновь возвращаются к третьему этапу, если все нули матрицы С_k⁽¹⁾ оказываются выделенными.

После конечного числа построений очередной первый этап обязательно закончится переходом на второй этап, и количество независимых нулей увеличится на единицу, т. е. (k+1) итерация будет завершена.