Исследуем функцию 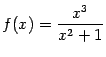 и построим её график.
и построим её график.
1). Поскольку знаменатель положителен при всех 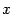 , область определения функции -- вся ось
, область определения функции -- вся ось 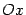 .
.
2). Функция 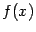 -- нечётная, поскольку при смене знака
-- нечётная, поскольку при смене знака 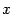 числитель меняет знак, а знаменатель остаётся без изменения, откуда
числитель меняет знак, а знаменатель остаётся без изменения, откуда 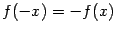 . Следовательно, график функции симметричен относительно начала координат.
. Следовательно, график функции симметричен относительно начала координат.
Периодической функция не является.
3). Поскольку область определения этой элементарной функции -- вся вещественная ось, вертикальных асимптот график не имеет.
4). Найдём наклонные асимптоты при 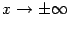 в виде
в виде 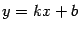 . Имеем:
. Имеем:
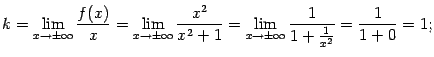
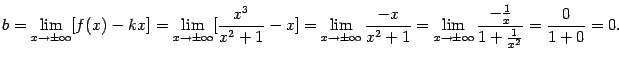
Таким образом, асимптотой как при 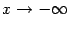 , так и при
, так и при 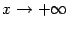 служит прямая
служит прямая 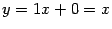 .
.
5). Найдём точки пересечения с осями координат. Имеем: 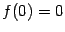 , причём
, причём 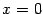 -- единственное решение уравнения
-- единственное решение уравнения 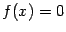 . Значит, график
. Значит, график 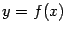 пересекает сразу и ось
пересекает сразу и ось 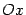 , и ось
, и ось 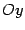 в начале координат.
в начале координат.
Очевидно, что 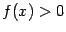 при
при 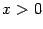 и
и 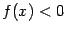 при
при 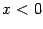 .
.
6). Найдём производную:
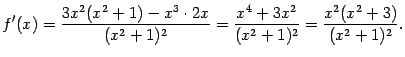
Очевидно, что 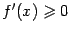 при всех
при всех 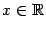 ; единственная точка, в которой
; единственная точка, в которой 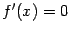 -- это
-- это 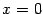 . Значит, функция
. Значит, функция 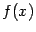 возрастает на всей оси
возрастает на всей оси 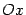 , а в стационарной точке
, а в стационарной точке 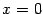 имеет горизонтальную касательную.
имеет горизонтальную касательную.
7). Найдём вторую производную:
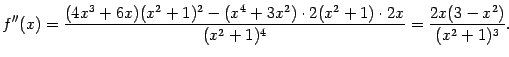
Знаменатель этой дроби положителен при всех 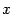 . Числитель имеет корни
. Числитель имеет корни 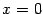 и
и 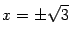 , при этом
, при этом 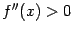 на интервалах
на интервалах 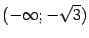 и
и 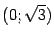 -- на этих интервалах функция выпукла. На интервалах
-- на этих интервалах функция выпукла. На интервалах 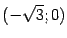 и
и 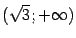 выполняется обратное неравенство
выполняется обратное неравенство 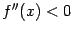 , здесь функция вогнута. Все три точки, в которых
, здесь функция вогнута. Все три точки, в которых 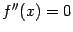 , то есть точки
, то есть точки 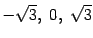 , являются точками перегиба.
, являются точками перегиба.
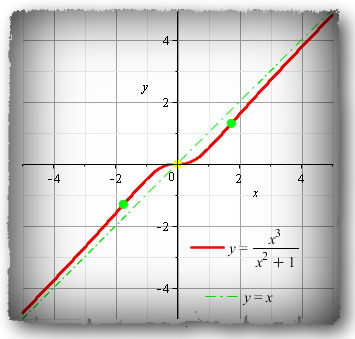
8). Теперь мы можем построить график с учётом всех предыдущих пунктов исследования функции. График имеет такой вид:
 2015-07-03
2015-07-03 475
475








