1. Построить вариационный ряд (расположить данные первичного ряда в порядке возрастания)
2. Пронумеровать значения вариационного ряда, начиная с меньшего значения. Меньшему значению присваивается первый номер
3. Рядом со значением записать его ранг, при этом:
а) если значение в вариационном ряду встречается единственный раз, то ранг равен порядковому номеру;
б) если значение в вариационном ряду встречается два или более раз, то ранг вычисляется как среднее из порядковых номеров, которые присвоены этому значению.
4. Правильность ранжирования можно проверить. Сумма рангов должна совпадать с расчетной: 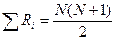
где N – количество значений в ранжируемом вариационном ряду.
Пример ранжирования.
Индивидуальные значения переменной «Х»: 2, 5, 6, 2, 5, 1, 3, 4, 4, 4.
Вариационный ряд «Х»: 1, 2, 2, 3, 4, 4, 4, 5, 5, 6
Данные вариационного ряда нумеруются. Определяется ранг значения, при этом, меньшему значению присваивается ранг равный единице. Значение «1» встречается в вариационном ряду единственный раз и имеет порядковый номер равный «1». Поэтому ранг значения «1» равен порядковому номеру, то есть R(1)=1. Значение «2» встречается в вариационном ряду два раза. Поэтому, ранг значения «2» вычисляется как среднее из порядковых номеров, на которых располагается это значение.
R(2)= 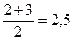
Значение «3» в вариационном ряду встречается единственный раз, поэтому ранг равен порядковому номеру. Ранг значения «3» равен четырем, то есть R(3)=4.
| № Порядковый номер | Х значение | R ранг |
| 2,5 | ||
| 2,5 | ||
| 8,5 | ||
| 8,5 | ||
| Сумма рангов |
Сумма рангов должна совпадать с расчетной: 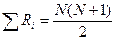
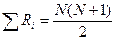 =
= 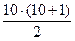 =1+2,5+2,5+4+6+6+6+4,5+4,5+10
=1+2,5+2,5+4+6+6+6+4,5+4,5+10
Процентиль – это процентная доля индивидов из выборки стандартизации, первичный результат которых ниже данного первичного показателя. Процентили показывают относительное положение каждого индивида в нормативной выборке, а не величину различия между результатами.
99 возможных процентилей (Р1,..Р99) делят множество наблюдений на 100 частей с равным числом наблюдений в каждой.
Например, если 28% людей правильно решают 15 задач в тесте на арифметическое мышление, то первичному показателю 15 соответствует 28-й процентиль (Р28).
Р-й процентильпредставляет собой точку, ниже которой лежит Р% оценок. 50-й процентиль (Р50) соответствует медиане. Процентили выше 50 представляют показатели выше среднего, а те, которые лежат ниже 50, - сравнительно низкие показатели.
Процентили указывают на относительное положение индивида в выборке стандартизации. Их также можно рассматривать как ранговые градации, общее число которых равно 100, с той разницей, что при ранжировании принято начинать отсчет сверху, то есть с лучшего члена группы, получающего ранг 1. В случае процентилей отсчет ведется снизу, так что, чем ниже процентиль, тем хуже позиция индивида.
Процентили не следует смешивать с обычными процентными показателям. Последние являются первичными показателями и представляют собой процент правильно выполненных заданий, тогда как процентиль – это производный показатель, указывающий на долю от общего числа членов группы. Первичный результат, который ниже любого показателя, полученного в выборке стандартизации, имеет нулевой процентильный ранг (Р0). Результат, превышающий любой показатель в выборке стандартизации, получает процентильный ранг 100 (Р100). Эти процентили, однако, не означают нулевого или абсолютного выполнения теста.
Перед началом вычисления любого процентиля в группе оценок надо упорядочить эти оценки по возрастанию. Для больших групп это непроизводительно и удобнее использовать сгруппированные данные.
Общая формула определения Рр -го процентиляв группе n оценок
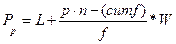
L - фактическая нижняя граница единичного интервала оценок, содержащего частоту p * n снизу распределения.
(cumf) - накопленная к L частота,
f - частота интервала оценок, содержащего частоту p*n.
W – ширина интервала оценок
Накопленные частоты к любой заданной оценке представляют собой суммарное количество частот на этой оценке или ниже ее.
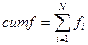
f - частота интервала оценок, содержащего частоту pn
Переход в шкалу Т-баллов: 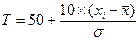
Где, xi-индивидуальное (i-е значение); 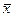 - среднее арифметическое; σ-стандартное отклонение.
- среднее арифметическое; σ-стандартное отклонение.
 2015-07-03
2015-07-03 14149
14149








