Пусть 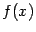 -- непрерывная функция, монотонная на интервале
-- непрерывная функция, монотонная на интервале 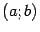 . Тогда, как мы доказали в гл. 3, функция
. Тогда, как мы доказали в гл. 3, функция 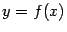 имеет обратную функцию
имеет обратную функцию  , которая также является непрерывной и монотонной функцией на интервале
, которая также является непрерывной и монотонной функцией на интервале 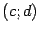 , в который функция
, в который функция 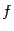 переводит интервал
переводит интервал 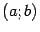 . Пусть
. Пусть 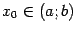 -- фиксированная точка и
-- фиксированная точка и 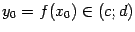 -- точка, ей соответствующая. Тогда
-- точка, ей соответствующая. Тогда 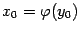 .
.
Теорема: Пусть функция 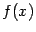 имеет в точке
имеет в точке 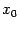 производную
производную 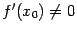 . Тогда обратная функция
. Тогда обратная функция 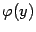 имеет в соответствующей точке
имеет в соответствующей точке 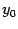 производную
производную 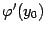 , которую можно отыскать по формуле
, которую можно отыскать по формуле
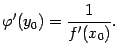
| (4.14) |
Доказательство. Дадим аргументу 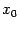 приращение
приращение 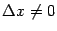 , такое что
, такое что 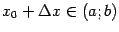 , и рассмотрим соответствующее приращение
, и рассмотрим соответствующее приращение 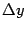 , определяемое равенством
, определяемое равенством 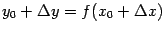 . Тогда, очевидно,
. Тогда, очевидно, 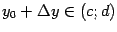 ; при этом
; при этом 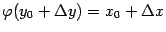 , а из монотонности функции
, а из монотонности функции 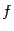 следует, что
следует, что 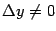 . Поскольку как функция
. Поскольку как функция 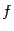 , так и функция
, так и функция 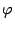 непрерывны, то условия
непрерывны, то условия 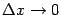 и
и 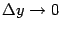 эквивалентны. Составим теперь разностное отношение для функции
эквивалентны. Составим теперь разностное отношение для функции  и запишем для него очевидное равенство:
и запишем для него очевидное равенство:
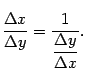
Теперь перейдём в этом равенстве к пределу при 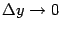 и учтём, что при этом
и учтём, что при этом 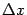 тоже стремится к 0:
тоже стремится к 0:
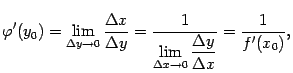
что мы и хотели доказать.
Заметим, что, очевидно, из формулы (4.14) следует, что
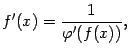
| (4.15) |
если 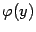 -- функция, обратная к
-- функция, обратная к 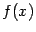 .
.
 2015-07-03
2015-07-03 251
251








