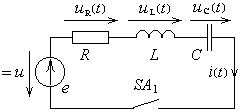
 Рис. 20.11. Подключение после- довательного соединения R, L, C к источнику постоянного напряжения. Рис. 20.11. Подключение после- довательного соединения R, L, C к источнику постоянного напряжения. |
Пример 3. Подключение последовательного соединения резистора, катушки и конденсатора к источнику постоянного напряжения (рис. 20.11).
Запишем полную систему расчетных уравнений цепи:
уравнение контура 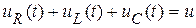 ,
,
уравнения элементов 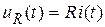 ,
, 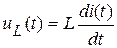 ,
, 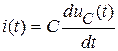 ,
, 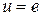 .
.
Подставляя выражение для тока из уравнения конденсатора в уравнения катушки и резистора, получим:
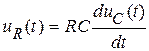 ,
, 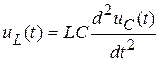 .
.
Подставим выражения для напряжений элементов в уравнение контура, получим дифференциальное уравнение переходного процесса для напряжения конденсатора:
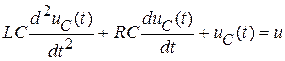 . (20.5)
. (20.5)
Для уравнения второго порядка нужны два начальных условия: 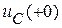 и
и 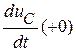 . При разомкнутом ключе начальное напряжение на конденсаторе может быть любым. Положим
. При разомкнутом ключе начальное напряжение на конденсаторе может быть любым. Положим 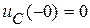 . По 2-му закону коммутации
. По 2-му закону коммутации 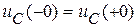 , поэтому
, поэтому 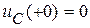 . До коммутации тока в цепи не было:
. До коммутации тока в цепи не было: 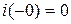 . Так как единственная ветвь цепи содержит катушку, то по первому закону коммутации
. Так как единственная ветвь цепи содержит катушку, то по первому закону коммутации 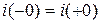 , значит,
, значит, 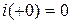 . Согласно уравнению конденсатора,
. Согласно уравнению конденсатора, 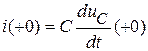 , поэтому
, поэтому 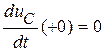 .
.
Решение 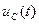 представим в виде суммы:
представим в виде суммы: 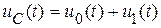 , где
, где 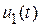 - частное решение уравнения (20.5). Это решение ищем в виде константы, что при подстановке в (20.5) дает
- частное решение уравнения (20.5). Это решение ищем в виде константы, что при подстановке в (20.5) дает 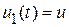 .
.
Функция 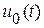 - это решение соответствующего однородного уравнения
- это решение соответствующего однородного уравнения
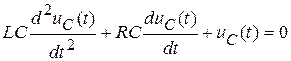 .
.
Она имеет вид
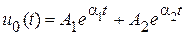 при
при 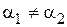 , (20.6)
, (20.6)
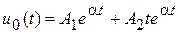 при
при 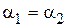 . (20.7)
. (20.7)
где α1 и α2 - корни характеристического уравнения 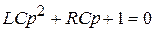 :
:
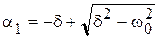 ,
, 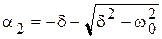 , здесь
, здесь 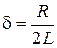 ,
, 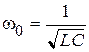 . (20.8)
. (20.8)
Рассмотрим отдельно три случая:
1. 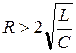 - апериодический процесс. При этом
- апериодический процесс. При этом 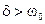 ,
, 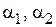 - действительные числа,
- действительные числа, 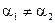 . График напряжения
. График напряжения 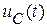 для R = 20 Ом, L = 10 мГн, C = 200 мкФ, е = 200 В показан на рис. 20.12.
для R = 20 Ом, L = 10 мГн, C = 200 мкФ, е = 200 В показан на рис. 20.12.
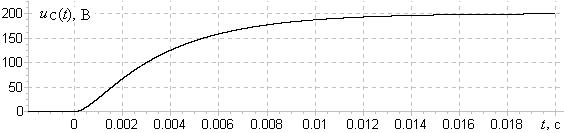 Рис. 20.12. Апериодический переходной процесс. Рис. 20.12. Апериодический переходной процесс. |
Рассчитаем значения коэффициентов α1 и α2 по формулам 20.8:
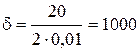 Гц,
Гц, 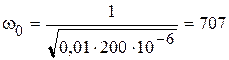 рад/с,
рад/с,
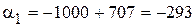 Гц,
Гц, 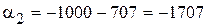 Гц.
Гц.
Подставим полученные коэффициенты в формулу (20.6) и потребуем выполнения начальных условий, учитывая, что 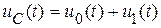 ,
, 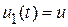 ,
, 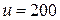 то есть,
то есть, 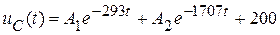 :
: 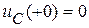 , следовательно,
, следовательно,
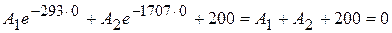 . (20.9)
. (20.9)
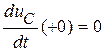 , следовательно, дифференцируя выражение для
, следовательно, дифференцируя выражение для 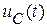 и приравнивая производную к нулю в момент t = 0, получим:
и приравнивая производную к нулю в момент t = 0, получим:
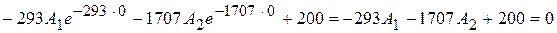 .(20.10)
.(20.10)
Решив совместно уравнения (20.9) и (20.20), получим: A 1 = -241,6 В, А 2 = 41,6 В.
Окончательно,
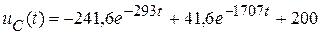 В.
В.
2. 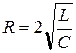 - критический процесс, пограничный между апериодическим и колебательным. При этом
- критический процесс, пограничный между апериодическим и колебательным. При этом 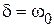 ,
, 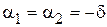 , процесс затухает за минимальное время. График напряжения
, процесс затухает за минимальное время. График напряжения 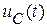 для R = 20 Ом, L = 10 мГн, C = 100 мкФ, е = 200 В показан на рис. 20.13.
для R = 20 Ом, L = 10 мГн, C = 100 мкФ, е = 200 В показан на рис. 20.13.
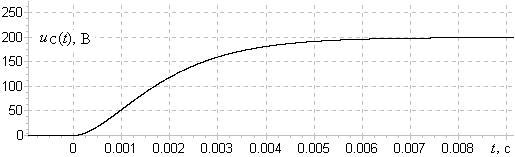 Рис. 20.13. Критический переходной процесс. Рис. 20.13. Критический переходной процесс. |
Найдем коэффициенты А 1 и А 2 в выражении для 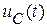 . В данном случае, с учетом формулы (20.7),
. В данном случае, с учетом формулы (20.7), 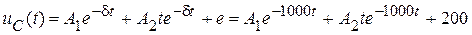 . Как и в случае периодического режима, потребуем выполнения начальных условий:
. Как и в случае периодического режима, потребуем выполнения начальных условий:
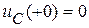 , следовательно,
, следовательно, 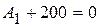 ,
, 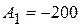 .
.
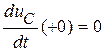 , следовательно, дифференцируя выражение для
, следовательно, дифференцируя выражение для 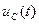 и приравнивая производную к нулю в момент t = 0, получим:
и приравнивая производную к нулю в момент t = 0, получим:
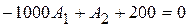 ,
, 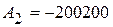 .
.
Окончательно получим:
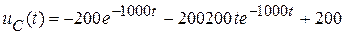 .
.
3. 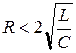 - колебательный режим. При этом
- колебательный режим. При этом 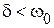 ,
, 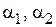 - пара сопряженных комплексных чисел. В этом случае решение однородного уравнения
- пара сопряженных комплексных чисел. В этом случае решение однородного уравнения 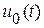 удобно представить в виде
удобно представить в виде
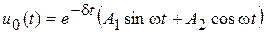 , (20.11)
, (20.11)
здесь 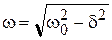 - частота собственных колебаний (см. п. 15).
- частота собственных колебаний (см. п. 15).
Тогда полное решение уравнения 20.5 будет выражаться формулой
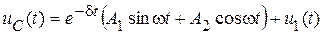 . (20.12)
. (20.12)
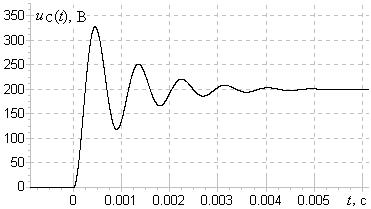 Рис. 20.14. Колебательный переходной процесс. Рис. 20.14. Колебательный переходной процесс. |
График этого напряжения для R = 20 Ом, L = 10 мГн, C = 2 мкФ, е = 200 В показан на рис. 20.14. Вычислим для этого набора исходных данных все коэффициенты в выражении (20.11). Как и в предыдущих случаях, 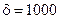 Гц,
Гц, 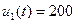 В.
В.
Далее, по формулам 20.8 и 20.11 получим:
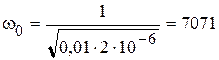 рад/с,
рад/с, 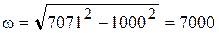 рад/с.
рад/с.
Рассчитаем коэффициенты А 1 и А 2, исходя из начальных условий.
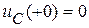 , следовательно,
, следовательно, 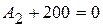 ,
, 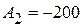 В.
В.
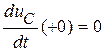 , следовательно, дифференцируя выражение для
, следовательно, дифференцируя выражение для 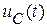 и приравнивая производную к нулю в момент t = 0, получим:
и приравнивая производную к нулю в момент t = 0, получим: 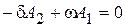 , то есть,
, то есть, 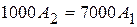 ,
, 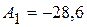 В.
В.
Окончательно: 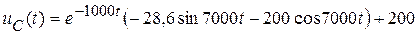 В.
В.
Замечание 3. Мы рассчитывали только одну величину для каждой задачи: напряжение конденсатора в 1 и 3 примерах и ток катушки во 2 примере. Все остальные напряжения и токи (например, напряжение катушки в примере 2) могут быть получены по результатам таких расчетов с помощью уравнений элементов и законов Кирхгофа.
Замечание 4. В настоящее время для расчета любых режимов электрических цепей обычно применяют численные алгоритмы, реализованные в виде различных компьютерных программ. Это очень удобно для практических расчетов, однако, инженеру нужно понимать теоретическую основу расчетов и знать особенности аналитических решений. Кроме того, надо иметь в виду, что компьютерные программы иногда выдают ошибочные решения, поэтому их нужно уметь каким-то способом контролировать.
 2015-07-03
2015-07-03 5181
5181








