2015-07-02
1405
Одним из путей решения уравнений, содержащих модуль, является графический метод.
Суть метода состоит в следующем. Решить уравнение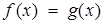 
– следовательно, найти все значения x, для которых значения функций 
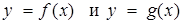равны, то есть найти абсциссы всех точек пересечения графиков этих функций. Если же графики не имеют общих точек, то уравнение не имеет корней.
Данный метод, реже других применяют для решения уравнений, содержащих модуль, так как он занимает достаточно много времени, не всегда рационален, результаты, полученные при построении графиков, не всегда являются точными. Кроме того, графическим методом можно решать уравнения с модулем любого вида, однако практическая реализация метода иногда бывает довольно сложной.
Следует также отметить, что точное построение графиков функций практически невозможно, поэтому решение, найденное графическим способом, требует проверки.
Проиллюстрируем применение графического метода для решения уравнений, содержащих переменную под знаком абсолютной величины.
Пример. Решим уравнение: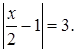 
Решение. Построим графики двух функций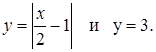 
Для построения графика функции 
, построим график вспомогательной функции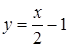 
– это прямая, пересекающая ось 
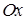в точке (2; 0), а ось 
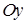в точке 
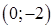, затем часть прямой, лежащую ниже оси 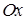зеркально отразить в оси .
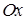Графиком функции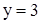 
является прямая, параллельная оси 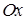и проходящая через точку (0; 3) на оси .
Графики функций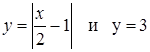 
представлены на рисунке 25.
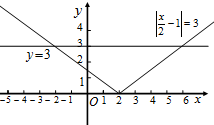Рис.25
Из рисунка 25 видно, что графики имеют две общие точки. Координаты одной точки: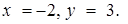 
Координаты другой: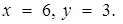 
Следовательно, исходное уравнение имеет два решения: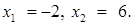 
Как отмечалось выше, при таком методе значения корней уравнения определяются приблизительно, и только проверка позволит доказать, что найденные значения действительно являются корнями исходного уравнения. При подстановке 
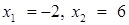в уравнение получаем, соответственно, два верных числовых равенства.
Ответ. .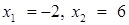
Пример. Решим уравнение: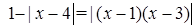 
Решение. Построим графики функци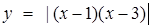й 
и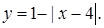 
Для построения графика функции 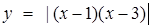построим график вспомогательной функции 
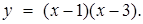График функции 
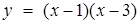пересекает ось 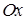в точках с абсциссами 
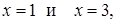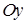ось в точке 
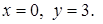Для построения графика функции 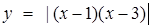часть графика вспомогательной функции 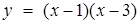, которая расположена ниже оси 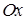симметрично отразим относительно данной оси вверх (Рис. 26)
Построим график функции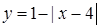 
с помощью преобразований графика элементарной функции 
Построим график вспомогательной функции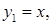 
затем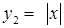 
симметричным отражением части графика вспомогательной функции 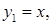которая расположена ниже оси 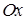, относительно данной оси вверх.
Строим график функции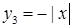 
симметричным отражением графика вспомогательной функции 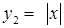относительно оси .
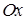Строим график функции 
сдвигом графика вспомогательной функции 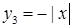, как жесткого тела на четыре единичных отрезка вправо.
Строим график функции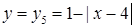 
сдвигом графика вспомогательной функции , как жесткого тела на один единичный отрезок вверх. График функции представлен на рисунке 26.
Графики функци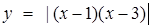й и 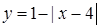пересекаются в одной точке 
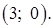Проверка показывает, что 
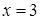– корень исходного уравнения.
Рис.26
Ответ.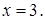 
Заметим, что при графическом методе решения не всегда удается найти точное значение корня, то применение данного метода бывает особенно эффективно, если требуется найти не сами корни, а определить их количество.
