Метод интервалов для решения уравнений, содержащих переменную под знаком абсолютной величины

Для решения уравнений и неравенств, содержащих модуль удобно применять метод интервалов.

Чтобы решить уравнение, необходимо раскрыть модули. Для этого выделяют интервалы, на каждом из которых выражения, стоящие под знаком модуля, принимают только положительные или только отрицательные значения. Отыскание таких интервалов основано на следующей теореме.

Теорема 8. Если на интервале 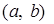функция 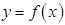непрерывна и не обращается в нуль, то на этом интервале она сохраняет знак.

Числовую ось разбивают на интервалы так, что по определению модуля, знак абсолютной величины на данных промежутках можно снять. Затем, для каждого из интервалов решают уравнение и делают вывод, относительно получившихся корней – удовлетворяют они нужному интервалу или нет.

Таким образом, для того, чтобы решить уравнение, содержащее неизвестную под знаком модуля, необходимо освободиться от знака модуля, используя его определение. Для этого следует:

– найти значения неизвестной, при которых выражения, стоящие под знаком модуля, обращаются в ноль;

– разбить область определения уравнения на промежутки, на каждом из которых выражения, стоящие под знаком модуля, сохраняют знак;

– на каждом из этих промежутков уравнение записать без знака модуля;

– решить полученные уравнения.

Объединение решений, найденных на всех промежутках, и составляет все решения исходного уравнения.

Проиллюстрируем метод интервалов для решения уравнений, содержащих переменную под знаком абсолютной величины, примерами.

Пример. Решим уравнение: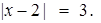

Решение. Чтобы выделить интервалы знакопостоянства, найдем точки, в которых выражения, записанные под модулем, обращаются в нуль: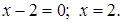

Получим два промежутка 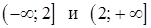. Определим знаки выражений на этих интервалах и на каждом из них решим уравнение.

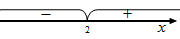
Получим две смешанных системы: 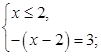и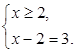

Решим каждую систему: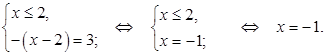

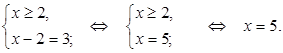
Ответ.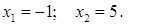

Пример. Рассмотрим метод интервалов на примере решения более сложного уравнения: .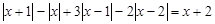

Решение. Чтобы выделить интервалы знакопостоянства, найдем точки, в которых выражения, записанные под модулем, обращаются в нуль:

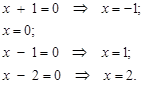
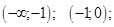
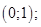
Полученные точки разбивают числовую ось на интервалы: 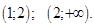Определим знаки выражений на этих интервалах (Рис. 23)

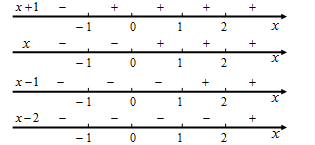Рис.23

Учитывая знаки, раскроем модули.

В результате получим совокупность систем, равносильную данному уравнению: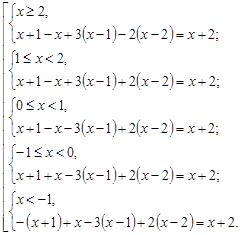

Последняя совокупность приводится к виду: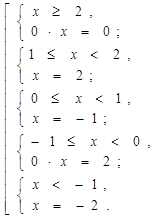

Решение совокупности систем и данного уравнения: 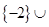[2;+¥).

Ответ. 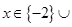[2;+¥).