Ситуация, связанная с необходимостью использования понятие модуля, возникает и при решении иррациональных уравнений.
Пример. Решим уравнение: 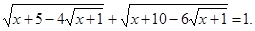
Решение. Введем новую переменную. Пусть 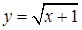 , где y
, где y 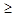 0,
0,
тогда 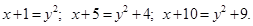
Данное уравнение примет вид: 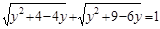 .
.
Последнее уравнение, равносильно 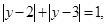 решая которое, методом интервалов, получим:
решая которое, методом интервалов, получим: 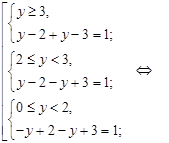
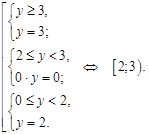
Таким образом, 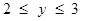 , то есть
, то есть 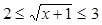 . Последнему неравенству удовлетворяют значения x, принадлежащие отрезку
. Последнему неравенству удовлетворяют значения x, принадлежащие отрезку 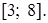
Ответ. 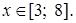
Напомним, что простейшие уравнения с модулем имеют вид: 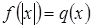 и
и 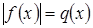 . Решим уравнения на основании определения модуля сведением к совокупности систем.
. Решим уравнения на основании определения модуля сведением к совокупности систем.
Пример. Решим уравнение: 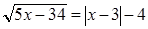 .
.
Решение. Чтобы выделить интервалы знакопостоянства, найдем точки, в которых выражения, записанные под модулем, обращаются в нуль: 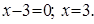
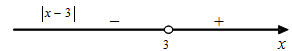
Уравнение равносильно совокупности двух систем: 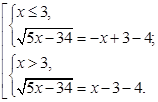
Решим каждую из систем.
Решение первой системы: 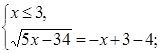
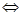
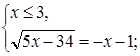
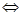
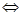
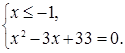
Полученная система не имеет корней, так как дискриминант уравнения 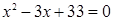 меньше нуля.
меньше нуля.
Решим вторую систему:
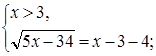
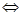
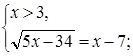
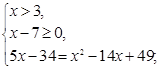
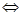
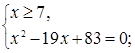
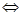
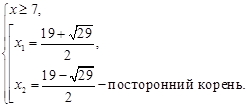
Ответ. 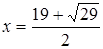 .
.
Пример. Решим уравнение: 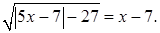
Решение. Чтобы выделить интервалы знакопостоянства, найдем точки, в которых выражения под модулем, обращаются в нуль: 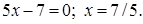
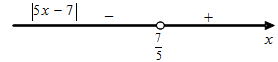
Уравнение равносильно совокупности двух систем: 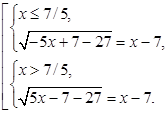
Решим первую систему:
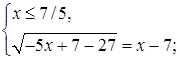
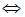
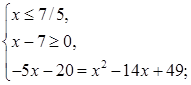
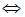
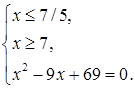
Пересечение множеств 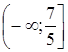 и
и  пусто. Следовательно, первая система совокупности корней не имеет.
пусто. Следовательно, первая система совокупности корней не имеет.
Решим вторую систему:
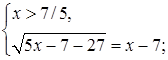
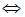
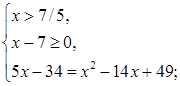
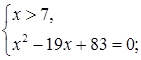
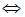
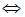
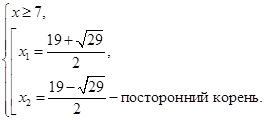
Ответ. 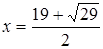 .
.
 2015-07-02
2015-07-02 3549
3549
