рис.46
На рисунку 46 крива y=f(x) – опукла в інтервалі (a, b), і угнута в інтервалі (c,d).
Означення 2. Точка, яка відділяє опуклу частину графіка функції від угнутої називається точкою перегину.
На рис.46 т. М – точка перегину з абсцисою х=b.
Інтервали опуклості і угнутості кривої знаходяться за допомогою слідуючої теореми.
Теорема 1. Нехай y=f(x) має похідні f¢(x) i f¢¢(x) в даному інтервалі. Тоді крива y=f(x) опукла в цьому інтервалі, якщо f¢¢(x)<0, i угнута, якщо f¢¢(x)>0, для всіх х з цього інтервала.
Так, напр., відповідно на рис.1 f¢¢(x)<0, якщо хÎ(a, b), f¢¢(x)>0, якщо хÎ(c, d).
Точки перегину знаходяться за наступною теоремою
Теорема 2. (Достатня умова точки перегину). Якщо 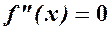 ,¥ або не існує і
,¥ або не існує і 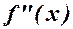 , змінює знак при переході через х0, то х0 є точкою перегину f(x).
, змінює знак при переході через х0, то х0 є точкою перегину f(x).
Приклад. Знайти проміжки проміжки опуклості, угнутості та точки перегину функції.
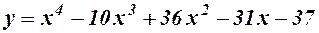 .
.
Розв’язання. Задана функція визначена для всіх 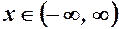 . Знайдемо її похідні
. Знайдемо її похідні
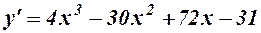 ,
,
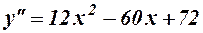 .
.
Щоб знайти інтервали опуклості і угнутості необхідно знайти корені другої похідної, які разом з точками розриву (якщо такі є) розбивають область існування на проміжки.
Якщо 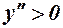 на проміжку, то графік угнутий;
на проміжку, то графік угнутий;
Якщо 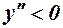 на проміжку, то графік опуклий.
на проміжку, то графік опуклий.
У тих точках, де друга похідна міняє знак, буде точка перегину, за умови, що функція в цій точці неперервна.
Отже, розв’язуємо рівняння 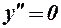
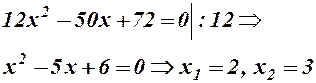
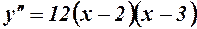 ;
;
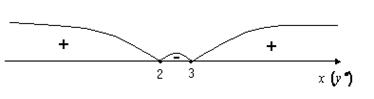
на 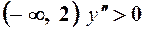 , графік угнутий;
, графік угнутий;
на 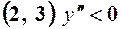 , графік опуклий;
, графік опуклий;
на 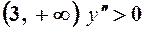 , графік угнутий.
, графік угнутий.
В точках 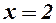 і
і 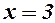 друга похідна міняє знак. Це є точки перегину.
друга похідна міняє знак. Це є точки перегину.
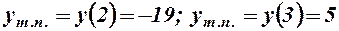 .
.
 2015-07-03
2015-07-03 416
416








