Асимптоти графіка функції

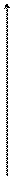
Означення. Пряма (l) називається асимптотою графіка функції (кривої (L)), якщо відстань MN від змінної точки кривої (MÎL) до прямої прямує до нуля, якщо точка М віддаляється в нескінченність, тобто 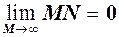(див. рис. 47,48)

Y Y

M

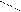M N

(L) N (L)

(l)

(l) X X

рис.47 рис.48

Асимптоти розрізняють:

1) вертикальні;

2) похилі (окремий їх випадок – горизонтальні).

1. Вертикальні асимптоти. Будемо говорити, що пряма х=а є вертикальною асимптотою графіка функції y=f(x), якщо хоча б одна з односторонніх границь функції дорівнює нескінченості при х®а±0, тобто

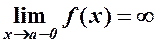, або .

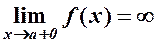Y

M N

x x=a X

2. Похилі асимптоти. Знаходяться у вигляді y=kx+b, де

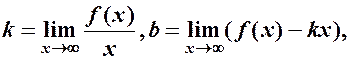
зокрема, якщо k=0, то отримуємо горизонтальну асимптоту y=b, де

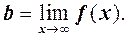
Приклади. Знайти асимптоти кривих:

1. 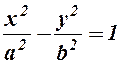. 2. .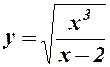

Розв’язання

1. Із рівняння 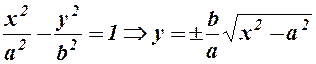. Функція існує для .

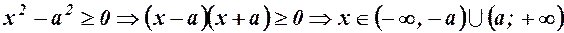Вертикальних асимптот функція немає оскільки при 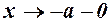і .

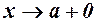
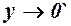Горизонтальних асимптот теж немає, бо .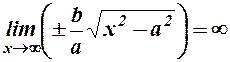

Знайдемо похилі асимптоти за формулою ,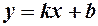

де .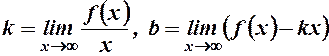

Знайдемо

;

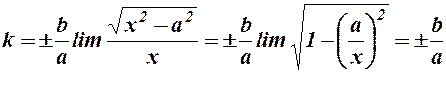Знайдемо вільний член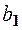

.

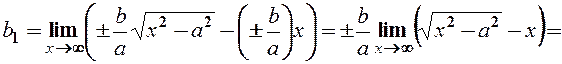
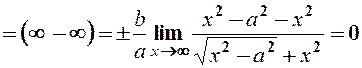Отже, отримали відомі рівняння асимптот гіперболи

.

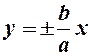2. 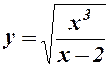. Дана функція визначена для 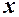, де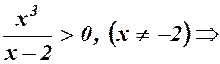

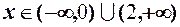
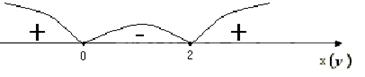
Оскільки

,

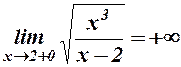то пряма 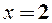є вертикальною асимптотою кривої.

Горизонтальних асимптот крива немає, оскільки

.

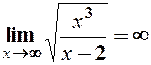Знаходимо похилі асимптоти 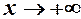при і при .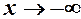

.

.

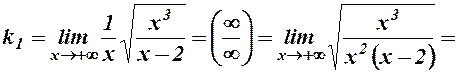
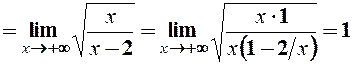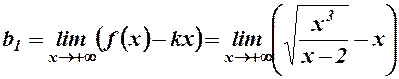
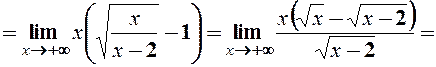
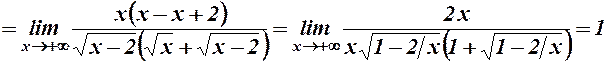Отже, існує права похила асимптота .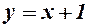

Знайдемо похилу асимптоту при .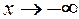

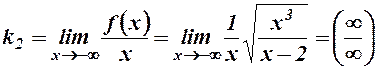
оскільки 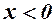, то 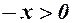- введемо під корінь

.

.

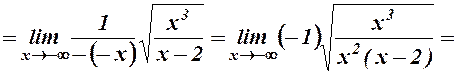
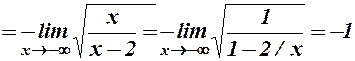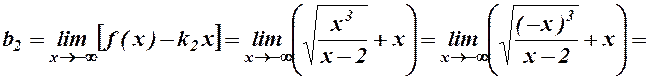
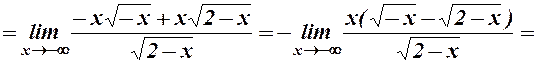
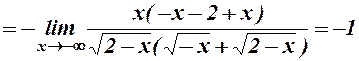Отже, 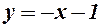- ліва похіила асимптота.

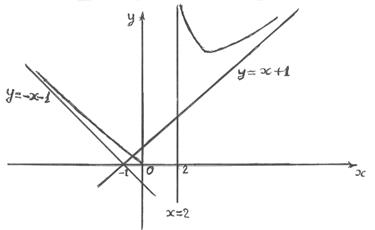
На рисунку зображені асимптоти та графік кривої.