«Как было многократно сказано ранее, любые расчеты на прочность и жесткость всегда начинаются с определения внутренних усилий, возникающих в элементе. Для нахождения внутренних усилий используют метод сечений, согласно которому, элемент мысленно рассекают плоскостью, одну его часть (любую) отбрасывают, действие отброшенной части на оставшуюся заменяют внутренними силами и для оставшейся части составляют уравнения равновесия. При статическом нагружении, когда нагрузка медленно и плавно прикладывается к элементу, возрастая от нуля до конечного значения, внутренние силы также нарастают очень медленно, поэтому в любое мгновение и затем на протяжении всего времени действия нагрузки между внешними и внутренними силами существует равновесие, и именно это обстоятельство позволяет для определения внутренних сил использовать уравнения статики. Таким образом, метод сечений предполагает РАВНОВЕСИЕ отсеченной части, что возможно только при статическом нагружении.
«Следует заметить, что при статическом нагружении все частицы при деформировании также перемещаются с ускорением. Но эти ускорения, а значит, и возникающие силы инерции ничтожно малы, поэтому в статических расчетах ими можно пренебречь.
«Однако при динамических нагрузках ускорения и силы инерции достаточно ощутимы, пренебрегать ими нельзя, а поэтому здесь нельзя также и говорить о равновесии системы, которое сохранялось бы на весь период действия нагрузки. Так как наличие ускорения предполагает, что скорость движущихся частиц в деформируемом теле в каждый момент времени изменяется, то здесь можно говорить только о МГНОВЕННОМ равновесии, т.е. о равновесии в данный момент времени, в данное мгновение. И такое мгновенное равновесие возможно, если к элементу вместе со всеми внешними нагрузками, включая реакции опор, приложить силу инерции, соответствующую данному мгновению. Этот прием решения всех динамических задач, связанный с учетом сил инерции, основан на принципе Даламбера, сформулированным в теоретической механике для материальной точки →
| Если в любой момент к каждой материальной точке системы приложить силу инерции этой точки, то эти силы инерции будут уравновешиваться всеми заданными силами, действующими на систему, включая реакции связей |
«Так как любое реальное тело можно представить как совокупность материальных точек, то приложив ко всем массам, движущимся с ускорением, помимо внешних активных и реактивных сил СИЛУ ИНЕРЦИИ этих масс, деформируемый элемент в каждый момент времени можно рассматривать в равновесии и применять для него обычные уравнения равновесия, используемые в статике.
| Поступательное движение |
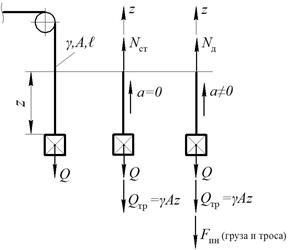
«Рассмотрим подъем груза 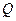 на тросе. Трос имеет длину
на тросе. Трос имеет длину 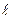 , площадь сечения А и выполнен из материала с удельным весом
, площадь сечения А и выполнен из материала с удельным весом 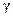 :
:
Вариант 1 – груз поднимается без ускорения (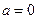 ) →
) →
В этом случае мы имеет статическое нагружение троса, он растягивается весом груза 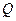 и весом оставшейся части троса
и весом оставшейся части троса 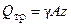 , в результате чего в сечении возникает статическая продольная сила
, в результате чего в сечении возникает статическая продольная сила 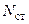 , определяемая из уравнения статики:
, определяемая из уравнения статики:
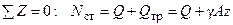 .
.
Вариант 2 – груз поднимается с ускорением (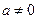 ) →
) →
В этом случае мы имеет динамическое нагружение троса, он растягивается весом груза 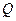 , весом оставшейся части троса
, весом оставшейся части троса 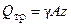 и силой инерции массы груза и массы части троса, равной
и силой инерции массы груза и массы части троса, равной
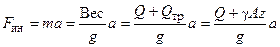 , где
, где 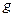 − ускорение свободного падения, равное 9,8 м/сек2.
− ускорение свободного падения, равное 9,8 м/сек2.
В результате этого в сечении возникает динамическая продольная сила 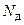 , определяемая на основании принципа Даламбера из уравнения статики:
, определяемая на основании принципа Даламбера из уравнения статики:
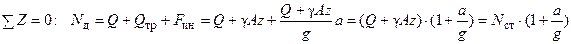 .
.
Введем обозначение → 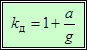 — называется динамический коэффициент.
— называется динамический коэффициент.
«И теперь используя динамический коэффициент, мы можем решать любые вопросы по определению напряжений и деформаций для этого класса задач →
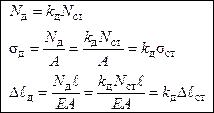
Таким образом, задачу можно полностью решать как статическую, определяя все необходимые параметры в статике − 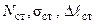 , а затем отдельно определить динамический коэффициент
, а затем отдельно определить динамический коэффициент 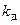 , ввести его в расчет и найти все динамические параметры −
, ввести его в расчет и найти все динамические параметры − 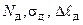 . Этот принцип будет использован и в других случаях динамических задач, когда динамический расчет может быть полностью сведен к статическому путем введения в расчет соответствующего динамического коэффициента.
. Этот принцип будет использован и в других случаях динамических задач, когда динамический расчет может быть полностью сведен к статическому путем введения в расчет соответствующего динамического коэффициента.
«Тогда условие прочности и жесткости для задач данного класса имеет вид →
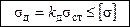 − условие прочности
− условие прочности
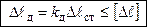 − условие жесткости,
− условие жесткости,
откуда также видно, что иногда динамический расчет можно целиком свести к статическому, понизив 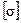 и
и 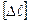 на величину
на величину 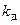 , т.е.
, т.е.
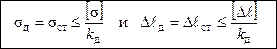 .
.
| Вращательное движение |
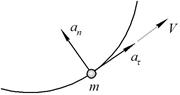 «Вращательное движение есть частный случай движения по кривой. При любом криволинейном движении возникают два ускорения →
«Вращательное движение есть частный случай движения по кривой. При любом криволинейном движении возникают два ускорения →
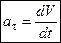 − тангенциальное ускорение, направлено по направлению
− тангенциальное ускорение, направлено по направлению
движения и характеризует изменение скорости 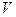 по величине;
по величине;
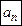 − радиальное ускорение, направлено к центру вращения и характеризует изменение скорости по направлению. При вращательном движении по окружности
− радиальное ускорение, направлено к центру вращения и характеризует изменение скорости по направлению. При вращательном движении по окружности 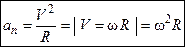 , где
, где 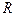 − радиус вращения;
− радиус вращения; 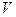 − линейная скорость;
− линейная скорость; 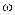 − угловая скорость, определяемая как
− угловая скорость, определяемая как 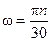 ,
,
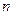 − число оборотов в минуту.
− число оборотов в минуту.
«Эти ускорения вызывают появление соответствующих сил инерции, которые воздействуют на элемент и вызывают появление в нем дополнительных напряжений и деформаций. Рассмотрим два случая вращательного движения – равномерное и неравномерное.
РАВНОМЕРНОЕ ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
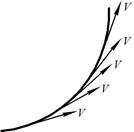 «Равномерное вращательное движение имеет место, когда тело вращается с постоянной скоростью, т.е.
«Равномерное вращательное движение имеет место, когда тело вращается с постоянной скоростью, т.е. 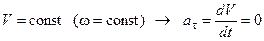 .
.
«Однако несмотря на то, что одно из ускорений равно нулю, вращательное движение является динамической нагрузкой, так как здесь всегда будет присутствовать радиальное ускорение 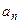 , отвечающее за изменение скорости по направлению, что всегда имеет место при движении по кривой.
, отвечающее за изменение скорости по направлению, что всегда имеет место при движении по кривой.
 2015-07-03
2015-07-03 1755
1755








