1. В ведомость вычисления координат (см. задания, табл. 3) из журнала полевых измерений (см. задания табл.1), для всех станций, начиная со второй, выписать значения горизонтальных углов bср. Значение угла, измеренного на точке 1 bср(1) (см. рис. 1) записывают на последней строке графы 2 табл. 3, заданий. Примычный угол (см. рис. 1) bприм = 152°18,5 из табл. 1 заданий выписать в ведомость вычисления координат (см. задания табл. 3) в графу 3 “Углы исправленные” в первую строку.
Пример вычислений в ведомости координат приведен в табл. 2 методических указаний.
2. Оценка точности угловых измерений. В ведомости вычисления координат определить сумму измеренных углов полигона (см. задания табл. 3, графа 2) и установить фактическую угловую невязку замкнутого теодолитного хода по формуле:
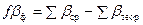 , (2)
, (2)
где 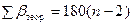 - теоретическая сумма углов в замкнутом многоугольнике.
- теоретическая сумма углов в замкнутом многоугольнике.
Вычислить допустимую невязку по формуле:
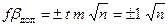 (3)
(3)
где n – количество углов теодолитного хода;
t – коэффициент значимости (t = 2);
m – средняя квадратическая погрешность измерения угла одним полным приемом (m= 0.5¢).
Если фактическая невязка, вычисленная по формуле (2) не превышает допустимой (fbдоп), установленной по формуле (3), то определить поправки в каждый измеренный угол по формуле:
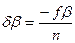 , (4)
, (4)
Поправки округляют до 0°00¢,1. При этом обязательным является условие:
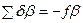 (5)
(5)
Оценку точности угловых измерений выполнить в табл. 3 заданий, под графой 2 – углы измеренные (пример вычислений см. табл. 2 методических указаний).
3. Вычислить значение исправленных углов. Для этого алгебраически суммируют величины измеренных углов и поправок к ним (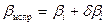 ) Результаты вычислений записывают в графу 3 табл. 3, см. задания. Вычислить сумму исправленных углов, которая должна равняться точно теоретической сумме углов
) Результаты вычислений записывают в графу 3 табл. 3, см. задания. Вычислить сумму исправленных углов, которая должна равняться точно теоретической сумме углов 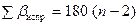 .
.
4. В ведомость вычисления координат (см. задания табл. 3, графа 4, первая строка) выписать индивидуальный для каждого студента дирекционный угол линии А-1(aA1), вычисленный по формуле (2).
5. Последовательно, начиная с дирекционного угла линии А-1 (aА1) примычному углу b прим = 152 18,5 и исправленным углам графы 3 (см. задания табл. 3), вычислить значения дирекционных углов всех последующих линий хода по формуле:
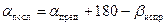 . (6)
. (6)
При этом, если в последовательности расчета получаются значения (aизм +180) < bизм, то необходимо использовать формулу:
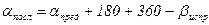
и если (aизм +180 - bизм,) > 360, то использовать формулу:
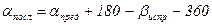 .
.
Результаты вычислений записать в графу 4 табл. 3 заданий. Контролем вычислений служит точное равенство величины дирекционного угла линии 1-2 (α12), вычисленного с использованием примычного угла bприм и того же дирекционного угла линии 1-2 (α12), последовательно вычисленного с использованием всех углов теодолитного хода.
6. Из табл. 2 (см. приложение) в ведомость вычисления координат (см. приложение, табл. 3) в столбец 5 выписать горизонтальные проложения, начиная с линии 1-2 (d12). В последнюю строку выписать расстояние линии 5-1 (d51). Вычислить сумму горизонтальных проложений 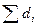 .
.
7. Вычислить приращения координат для всех сторон хода по формулам:
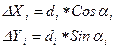 (7)
(7)
При использовании калькулятора вычисления выполняют в следующей последовательности, например, необходимо вычислить:
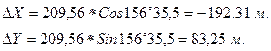
На калькуляторе
для вычисления DX набираем: 35,5:60+156= Cos *209.56 = -192.31 м.;
для вычисления DY набираем: 35,5:60+156= Sin *209.56 = 83.25 м.
Результат, полученный на индикаторе калькулятора округлить до 0,01 м и запасать ΔX в графу 6 и ΔY в графу 7 см. задания табл.3.
8. Выполнить оценку точности линейных измерений. Для этого вычислить сумму приращений координат 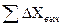 и
и 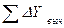 и установить невязки по формулам:
и установить невязки по формулам:
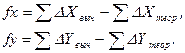 (8)
(8)
При этом принять во внимание, что в замкнутом полигоне 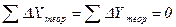 .
.
Вычислить абсолютную и относительную невязки:
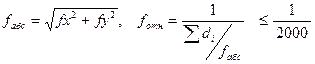 (9)
(9)
где 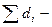 сумма всех сторон замкнутого теодолитного хода.
сумма всех сторон замкнутого теодолитного хода.
Если полученное значение относительной невязки не превышает заданного предела fотн ≤ fотн(доп) = 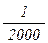 , то можно продолжить вычисления.
, то можно продолжить вычисления.
Суммы горизонтальных проложений и приращений координат записывают в нижней части граф 5, 6 и 7 см. задания табл. 3, а оценку точности теодолитного хода (вычисление абсолютной и относительной невязки) в нижней части ведомости вычисления координат (см. задания табл. 3).
9. Вычислить поправки в приращения координат по формулам:
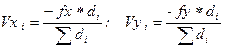 . (10)
. (10)
Поправки округлить с точностью до 0,01 м и записать Vx в графу 8, Vy в графу 9 табл. 3 заданий. При этом обязательным является выполнение условий:
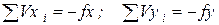 . (11)
. (11)
10. Найти исправленные значения приращений. Для этого суммировать величины вычисленных приращений координат и поправок с учетом их знаков. Результаты записать: DXиспр в графу 10 и DYиспр в графу 11 см. задания табл. 3.
11. Вычислить значения координат всех точек теодолитного хода. Для этого координаты точки 1, заданной преподавателем (см. решение обратной геодезической задачи), выписать в табл. 3 заданий (X – графа 12, Y – графа 13, вторая строка). Координаты точек 2,3,4,5 определяют путем последовательного алгебраического сложения координат предыдущей точки с исправленными приращениями координат.
Xпосл = Xпред + DXиспр
Yпосл = Yпред + DYиспр
Контролем вычислений служат значения координат первой точки, которые получаются вторично из последовательного сложения. Результаты вычислений записать: X в графу 12, Y в графу 13 см. задания табл. 3.
Построение плана теодолитной съёмки
На чертёжной бумаге размером ½(А-1), построить сетку квадратов со стороной 10 см. Полученные квадраты проконтролировать путем прикладывания линейки по диагонали квадратов. При этом все вершины сетки квадратов должны лежать на одной прямой линии.
План участка местности составить в масштабе 1:2000 (1 см. на плане соответствует 20 метрам на местности). На рис. 2 методических указаний приведен пример оформления плана участка местности. Объекты местности (опоры ЛЭП, здание, изгороди, электроподстанцию, дорогу и т.п.) в соответствии с абрисом теодолитной съемки (см. задания рис. 2) каждый студент наносит на индивидуальный план самостоятельно. При определении на плане точек местности необходимо использовать дополнительные линии, которые должны быть удалены сразу после определения положения точек местности. Составление плана выполнить в следующей последовательности (см. рис. 2 методических указаний).
- Принять за положительное направление оси абсцисс координату Y и за положительное направление оси ординат координату X. При этом ордината Х имеет направление на север (см. рис. 2).
- В соответствии с координатами по индивидуальной ведомости координат студента (см. задания табл. 3) оцифровать сетку квадратов числами кратными 0,2 километра. Оцифровку выполнить так чтобы полигон, с координатами вершин (по индивидуальной ведомости студента, см. задания табл. 3) расположился примерно в середине листа чертёжной бумаги размером ½ (А-1).
- В соответствии с координатами точек, вычисленными в индивидуальной ведомости координат студента (см. задания табл. 3), последовательно нанести на план все точки теодолитного хода. Для этого по координатам, например точки 1, определить квадрат, в котором она расположена. Отложив соответствующие расстояния от сетки квадратов по направлениям осей координат, нанести на план точку 1, затем, поступая аналогично, нанести точку 2, затем точку 3. И так все пять точек. Нанесенные на план точки соединить прямыми линиями (см. рис. 2).
- В соответствии с абрисом – глазомерным рисунком местности (см. задания рис. 2), составить точный план теодолитной съемки. При этом использовать метод перпендикуляров (прямоугольных координат), метод полярных координат, метод угловых засечек, метод линейных засечек и метод створов.
Метод перпендикуляров (прямоугольных координат, рис. 3) заключается в отложении расстояния (см. рис. 3, 125,8 м) в масштабе составляемого плана от точки теодолитного хода (см. рис. 3, точка II) по направлению линии этого хода до точки, определяющей основание перпендикуляра. В этой точке восстанавливается перпендикуляр к направлению линии теодолитного хода и по направлению перпендикуляра откладывается длина (см. рис. 3, 38,2 м), указанная на абрисе. Таким способом полученная на плане точка является либо углом контура объекта (например, изгороди, см. рис. 3), либо опорой линии электропередачи, либо иным объектом местности (см. задания, рис. 2).
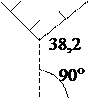 |
|


 II III
II III Рис. 3. Схема съемки методом перпендикуляров
(прямоугольных координат)
Метод полярных координат (рис. 4) заключается в отложении угла по ходу часовой стрелки от полярной оси и отложения расстояния по направлению отложенного угла в масштабе плана. Откладываемые угол и расстояние являются полярными координатами искомой на плане точки. Например (см. рис. 4), значения b = 23° 25¢ и d = 60,6 м и b = 69°28¢ d = 72,5 м являются полярными координатами оси асфальтированной дороги (см. задания, рис. 2).
За полюс в полярной системе координат принимаются точки теодолитного хода (см. рис. 4, точка IV), а за полярные оси направления линий того же теодолитного хода (см. рис. 4, направление линии IV – III).
На абрисе (см. рис. 2 заданий) направления полярных осей показаны стрелками. Точки, полученные на плане методом полярных координат, являются либо осью дороги (см. рис. 4), либо углом контура объекта (например, забора), либо опорой линии электропередачи, либо иным объектом местности (см. абрис, рис. 2 заданий).
| |||||
 | |||||
 | |||||
|
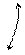


 IV III
IV III 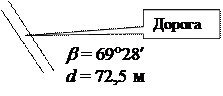 |
Рис. 4. Схема съемки методом полярных координат
Метод угловых засечек (рис. 5) заключается в отложении двух углов bIV и bV (см. рис. 5) от одной и той же полярной оси (линии теодолитного хода) с противоположных ее концов. Углы откладывают по ходу часовой стрелки. Направления полярных осей на абрисе (см. рис. 2 заданий) показаны стрелками. В пересечении линий при отложении углов получают точку, которая является либо опорой линии электропередачи (см. рис. 5), либо углом контура объекта (например, дома), либо иным объектом местности (см. абрис, рис. 2 заданий).
 |


 IV V
IV V
Рис. 5. Схема съемки методом прямой угловой засечки
Метод линейных засечек (рис. 6) заключается в отложении двух расстояний (радиусов окружности R1 и R2 см. рис. 6) в масштабе составляемого плана от точек, разнесенных на некоторое расстояние (базис см. рис. 6). За базис может приниматься любая прямая линия местности известной длины. Например, прямолинейный участок изгороди, часть линии теодолитного хода, длина стены здания и т.п. При отложении радиусов пользуются циркулем, с помощью которого делают засечки на расстояниях указанных на абрисе (см. рис. 6 и рис. 2 заданий) сначала от одного конца базиса, затем от другого. В пересечении дуг получают точку, которая является либо опорой линии электропередачи (см. рис. 6 и рис. 2 заданий), либо углом здания, либо иным объектом местности.
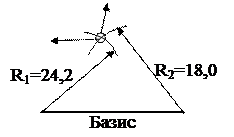
Рис. 6. Схема съемки методом линейной засечки
Метод створов (рис. 7) заключается в отложении расстояния (см. рис. 7, d = 176.8) в масштабе составляемого плана от точки теодолитного хода (см. рис. 7, точка I) по направлению линии этого хода (см. рис. 7, направление линии I – II) до точки пересечения этой линии с объектом местности. Например, с линией электропередачи (см. рис. 7), линией связи, дорогой или иным линейным объектом (см. задания, рис. 2).
 |
|
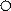

 I II
I II 
Рис. 7. Схема съемки методом створов
Оформление плана участка местности (см. рис. 2). Используя методы определения точек местности относительно точек и линий теодолитного хода построить план участка местности и оформить его в соответствии с условными знаками. При этом все вспомогательные линии, с помощью которых определялось положение на плане того или иного объекта местности, следует удалить.
Построенный план участка местности обводится рамкой. По внешнему контуру рамки подписываются выходы координатной сетки в километрах. По полю плана координатная сетка оставляется в виде пересечений (крестиков) с длиной линий 2 см.
На свободном месте плана напротив каждой линии теодолитного хода в виде правильной дроби подписываются значения румба (числитель) и горизонтальное проложение линии (знаменатель). Также на свободном месте плана вычерчивается линейный и ниже его, численный масштаб. В правом (левом) верхнем углу вычерчивается стрелка указывающая направление на север.
 2015-07-04
2015-07-04 1493
1493