Графический способ
Лекция 4. Определение плановых координат точек местности
Любой объект на местности можно описать с помощью координат точек, принадлежащих этому объекту.
• проводятся измерения на местности
• на бумаге в масштабе карты наносятся результаты измерений
• получается положение точки на карте
Неприменим для построения геодезических сетей из-за своей малой точности.
• проводятся определенные измерения на местности
• по измеренным значениям с помощью формул вычисляются координаты точки
Мы уже упоминали понятие точности. Прежде чем перейти к вопросу о геодезических измерениях, остановимся на нем подробнее.
Точность измерений выражает степень близости результата измерений к действительному значению измеряемой величины. Абсолютно точные измерения невозможны в силу комплекса причин. Измерения происходят в конкретных условиях, которые, в свою очередь, определяются факторами (внешней среды, объекта измерений, исполнителя, средств измерений). В процессе работы факторы не сохраняют стабильности, что и приводит к отклонению результата от истинного значения. Это отклонение называют погрешностью измерений.
Если условия измерений остаются, насколько это возможно, постоянными (одно средство измерения, один и тот же исполнитель), то говорят о равноточных измерениях.
Чтобы оценить точность измерений, необходимо классифицировать погрешности по природе их возникновения. Различают три вида погрешностей:
Грубые. Возникают в основном из-за ошибок человека, производящего измерения. Возможны в случае непредвиденного выхода из строя измерительного инструмента. Для исключения грубых погрешностей используют специальную методику измерений (контрольные отсчеты по разным счетным шкалам), специальные правила записи результатов измерений.
Систематические. Связаны с точностью инструментов и состоянием окружающей среды. Имеют явно выраженный закономерный характер, остаются постоянными на протяжении длительного времени или изменяются по определенному закону.
Систематические погрешности стремятся обнаружить и исключить посредством поверки инструментов, т.е. выполнения серии измерений эталонной величины. При обнаружении систематических погрешностей инструмент исправляют (юстировка) или вводят необходимые поправки в результаты измерений.
Случайные. Причинами могут быть остаточные систематические погрешности, несовершенство органов чувств человека, некоторые природные факторы и т.п. Эти погрешности имеют следующие свойства: их численные значения небольшие по абсолютной величине, появление положительных и отрицательных погрешностей равновероятно, малые по модулю значения встречаются значительно чаще, чем большие, чем больше ряд наблюдений, тем больше сумма погрешностей стремится к нулю.
Если проведены несколько (n) измерений одной и той же величины a (например, угла). При этом каждый раз получаются немного отличные друг от друга значения (a1, a2, a3 и т.д.) то:
Среднее арифметическое значение числа
аср = (а1+a2+a3+…+an) / n = ∑an / n
Среднее арифметическое конечного ряда случайных величин есть наиболее вероятное значение измеряемой величины. Это свойство среднего арифметического дает возможность отыскать наиболее точное значение определяемых величин из ряда многократных измерений, содержащих случайные погрешности.
Качество измерений устанавливает показатель «разброса» результатов относительно их среднего арифметического.
Средняя квадратическая погрешность измерений:
M = ± √ ∑∆an2 / (n-1), где ∆an= an - аср
Установлено, что из 1000 равноточных независимых измерений 68 % случайных погрешностей не превышают значений M, 95,4 % - 2М, 99,7 % - 3М, лишь 0,3 % больше. Эта закономерность дает возможность установить предельно допустимое значение случайных погрешностей, например, для геодезических измерений 2,5 М.
Результатом влияния погрешностей на точность измерений являются невязки, т.е. расхождение теоретически вычисленных значений с измеренными. Невязки так же, как и погрешности, присутствуют при любом виде геодезических работ. Для каждого вида работ и класса точности невязкине должны превышать величин, установленных стандартами.
Выделяют несколько способов определения плановых координат. Основные – геодезические засечки, полигонометрия (геодезические ходы), триангуляция. Начнем с последнего.
Триангуляция – способ передачи плановых координат, основанный на измерении внутренних углов треугольника. Для вычисления координат точек в сети триангуляции необходимо иметь исходные данные: координаты двух точек в треугольнике.
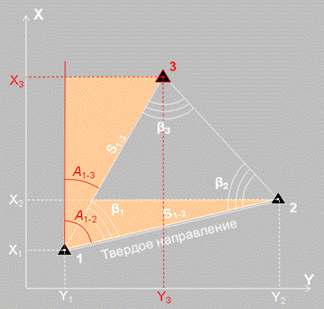
Из прямоугольного треугольника:
S1-2=(∆Y1-2)2+(∆X1-2)2
Α 1-2= arctg (∆Y1-2/ ∆X1-2)
Обратная геодезическая задача
Α 1-3= Α 1-2 – β1
По теореме синусов:
S1-3/sinβ1= S1-2/sinβ3
S1-3= sinβ1*S1-2/sinβ3
Из прямоугольного треугольника:
∆X1-3= S1-3*cos Α 1-3
∆Y1-3= S1-3*sin Α 1-3
Прямая геодезическая задача
Для измерения горизонтальных и вертикальных углов на местности служат теодолиты. Точность теодолитов определяется средней квадратической погрешностью измерения горизонтального угла в лабораторных условиях. Значения погрешности указывает в маркировке инструмента. Например, теодолит Т30 предназначен для измерения углов с погрешностью 30” и т.д.
К основным узлам оптических теодолитов относятся: ориентирующее устройство (зрительная труба), угловые рабочие меры (горизонтальный и вертикальный лимбы), осевая система, отсчетные устройства. Подставка (трегер) с подъемными винтами предназначена для крепления теодолита к штативу, его центрирования и горизонтирования. Центрирование может проводиться с помощью отвеса или оптического центрира. Верхняя часть теодолита называется алидадой. Она свободно вращается относительно подставки.
Зрительная труба предназначена для наведения теодолита на отдаленные цели. Она имеет объектив и окуляр с встроенной сеткой нитей.
Лимбы в теодолитах располагают в двух взаимно перпендикулярных плоскостях: горизонтальный и вертикальный круг. Лимбы выполняются в виде стеклянных круговых пластин с выгравированными штрихами градусной меры от 0 до 360.
Счетная система представляет собой систему призм, с помощью которой в поле зрения отсчетного микроскопа выводятся градусные фрагменты лимбов в соответствии с текущей ориентацией зрительной трубы.
Осевая система теодолита включает вертикальную ось (ось вращения алидады), ось вращения зрительной трубы и ось визирования.
При установке теодолита в рабочее положение горизонтальную линию задает ось уровня горизонтального круга – цилиндрический уровень. Поверка цилиндрического уровня – горизонтирование инструмента. Порядок выполнения. 2с.
Измерение горизонтальных углов – углов, лежащих в плоскости горизонта с вершиной в точке измерения между направлениями на местности из этой точки на две другие. Условия для измерений выбирают оптимальные, исключают рефракцию, плохую видимость. Полуприем, полный прием. Контроль 2с. Два значения угла. При допустимых 2с берут среднее как наиболее точное.
Полигонометрия заключается в разбивке полигонов на местности и прокладывании теодолитных ходов по точкам полигонов. Теодолитные ходы бывают трех видов.
Замкнутый ход начинается и заканчивается в твердой точке.
Разомкнутый прокладывается между двумя твердыми точками.
Висячий ход в случае необходимости продолжают от некоторых точек теодолитного хода для определения координат точек, находящихся в стороне от основного хода. Вследствие бесконтрольности не делают большой протяженности (300-400 м).
Предельная длина теодолитного хода зависит от точности определения координат и масштаба составляемой карты. 1: 2 000 – периметр 2-3 км, 1: 25 000 – 10-15 км.
Схема теодолитного хода
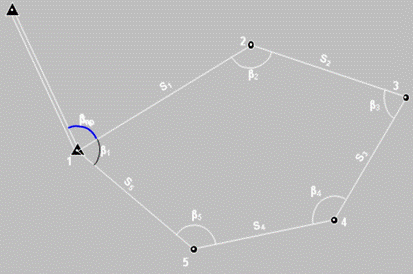
∑βт = 180° * (n-2)
∑β = β1 + β2 + …+ βn
Угловая невязка fβ = ∑β - ∑βт
Допустимая угловая невязка fβдоп = 2m√n, где m – точность прибора, n – число углов хода
Измерения в теодолитном ходе
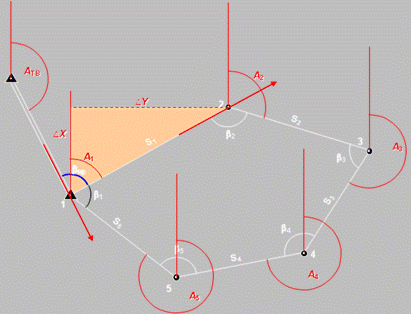
A1 = AТВ +180° + βпр A n+1 = A n +180° - βn+1
∆X = S * cos A ∆Y = S * sin A
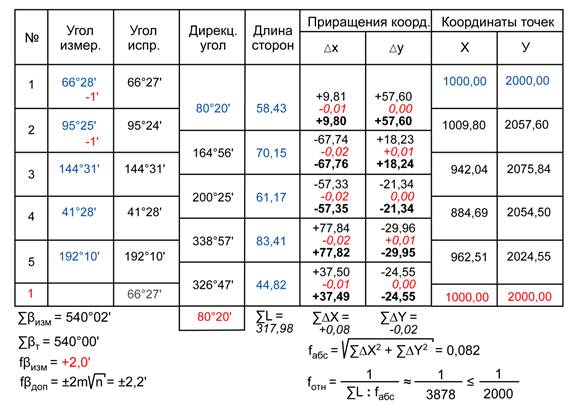
Ведомость вычисления координат точек теодолитного хода
 2014-02-02
2014-02-02 7516
7516
