Площадь

Площадь произвольного не самопересекающегося четырёхугольника с диагоналями 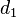, 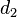и углом 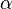между ними (или их продолжениями), равна:

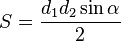
Площадь произвольного выпуклого четырёхугольника равна:

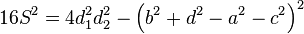· , где 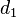, 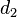— длины диагоналей, a, b, c, d — длины сторон.

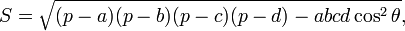·: где p — полупериметр, а 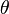есть полусумма противоположных углов четырёхугольника. (Какую именно пару противоположных углов взять роли не играет, так как если полусумма одной пары противоположных углов равна 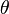, то полусумма двух других углов будет 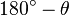и 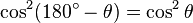). Из этой формулы для вписанных 4-угольников следует формула Брахмагупты.